Question Number 103703 by mohammad17 last updated on 16/Jul/20
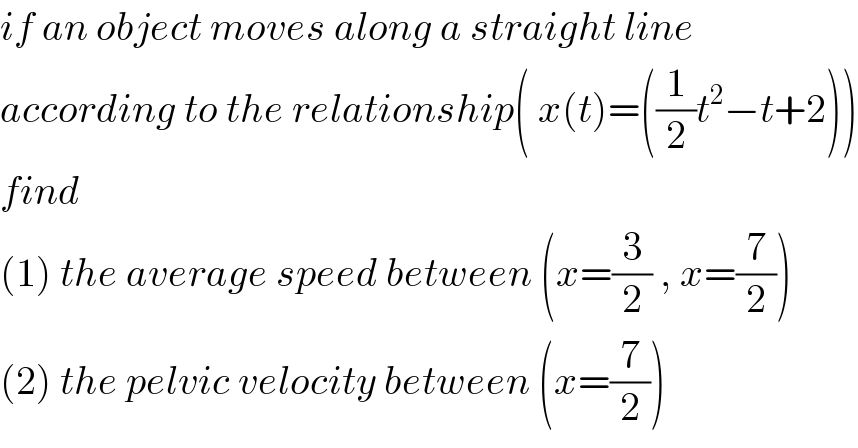
$${if}\:{an}\:{object}\:{moves}\:{along}\:{a}\:{straight}\:{line}\: \\ $$$${according}\:{to}\:{the}\:{relationship}\left(\:{x}\left({t}\right)=\left(\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} −{t}+\mathrm{2}\right)\right) \\ $$$${find}\: \\ $$$$\left(\mathrm{1}\right)\:{the}\:{average}\:{speed}\:{between}\:\left({x}=\frac{\mathrm{3}}{\mathrm{2}}\:,\:{x}=\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$$$\left(\mathrm{2}\right)\:{the}\:{pelvic}\:{velocity}\:{between}\:\left({x}=\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 16/Jul/20
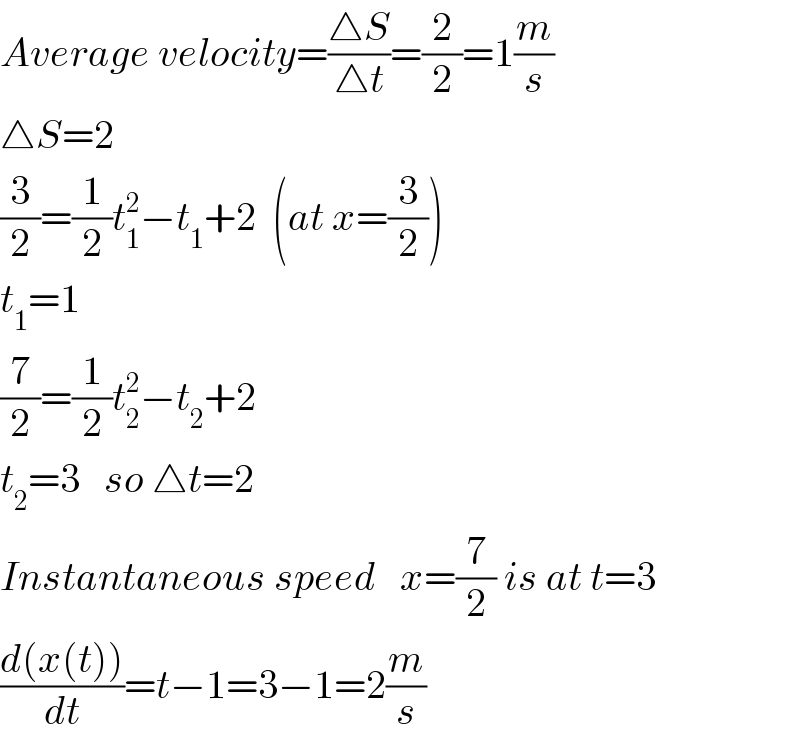
$${Average}\:{velocity}=\frac{\bigtriangleup{S}}{\bigtriangleup{t}}=\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1}\frac{{m}}{{s}} \\ $$$$\bigtriangleup{S}=\mathrm{2} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{t}_{\mathrm{1}} ^{\mathrm{2}} −{t}_{\mathrm{1}} +\mathrm{2}\:\:\left({at}\:{x}=\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$${t}_{\mathrm{1}} =\mathrm{1} \\ $$$$\frac{\mathrm{7}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{t}_{\mathrm{2}} ^{\mathrm{2}} −{t}_{\mathrm{2}} +\mathrm{2} \\ $$$${t}_{\mathrm{2}} =\mathrm{3}\:\:\:{so}\:\bigtriangleup{t}=\mathrm{2} \\ $$$${Instantaneous}\:{speed}\:\:\:{x}=\frac{\mathrm{7}}{\mathrm{2}}\:{is}\:{at}\:{t}=\mathrm{3} \\ $$$$\frac{{d}\left({x}\left({t}\right)\right)}{{dt}}={t}−\mathrm{1}=\mathrm{3}−\mathrm{1}=\mathrm{2}\frac{{m}}{{s}} \\ $$
