Question Number 19367 by Tinkutara last updated on 10/Aug/17
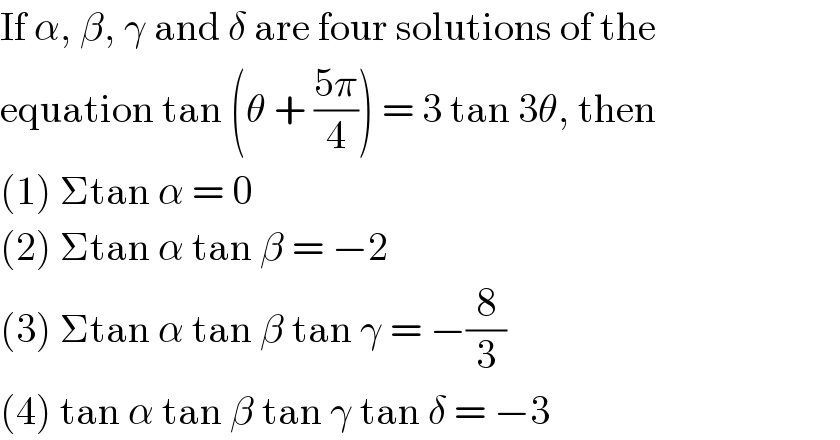
$$\mathrm{If}\:\alpha,\:\beta,\:\gamma\:\mathrm{and}\:\delta\:\mathrm{are}\:\mathrm{four}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mathrm{tan}\:\left(\theta\:+\:\frac{\mathrm{5}\pi}{\mathrm{4}}\right)\:=\:\mathrm{3}\:\mathrm{tan}\:\mathrm{3}\theta,\:\mathrm{then} \\ $$$$\left(\mathrm{1}\right)\:\Sigma\mathrm{tan}\:\alpha\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\Sigma\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta\:=\:−\mathrm{2} \\ $$$$\left(\mathrm{3}\right)\:\Sigma\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta\:\mathrm{tan}\:\gamma\:=\:−\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta\:\mathrm{tan}\:\gamma\:\mathrm{tan}\:\delta\:=\:−\mathrm{3} \\ $$
Answered by ajfour last updated on 10/Aug/17
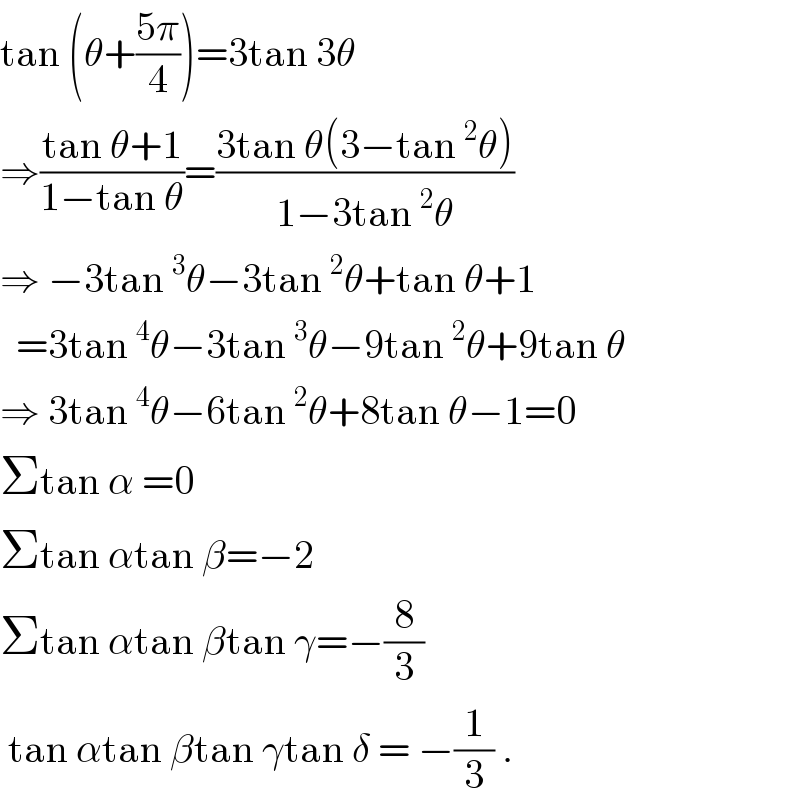
$$\mathrm{tan}\:\left(\theta+\frac{\mathrm{5}\pi}{\mathrm{4}}\right)=\mathrm{3tan}\:\mathrm{3}\theta \\ $$$$\Rightarrow\frac{\mathrm{tan}\:\theta+\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:\theta}=\frac{\mathrm{3tan}\:\theta\left(\mathrm{3}−\mathrm{tan}\:^{\mathrm{2}} \theta\right)}{\mathrm{1}−\mathrm{3tan}\:^{\mathrm{2}} \theta} \\ $$$$\Rightarrow\:−\mathrm{3tan}\:^{\mathrm{3}} \theta−\mathrm{3tan}\:^{\mathrm{2}} \theta+\mathrm{tan}\:\theta+\mathrm{1} \\ $$$$\:\:=\mathrm{3tan}\:^{\mathrm{4}} \theta−\mathrm{3tan}\:^{\mathrm{3}} \theta−\mathrm{9tan}\:^{\mathrm{2}} \theta+\mathrm{9tan}\:\theta \\ $$$$\Rightarrow\:\mathrm{3tan}\:^{\mathrm{4}} \theta−\mathrm{6tan}\:^{\mathrm{2}} \theta+\mathrm{8tan}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$$\Sigma\mathrm{tan}\:\alpha\:=\mathrm{0} \\ $$$$\Sigma\mathrm{tan}\:\alpha\mathrm{tan}\:\beta=−\mathrm{2} \\ $$$$\Sigma\mathrm{tan}\:\alpha\mathrm{tan}\:\beta\mathrm{tan}\:\gamma=−\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\:\mathrm{tan}\:\alpha\mathrm{tan}\:\beta\mathrm{tan}\:\gamma\mathrm{tan}\:\delta\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\:. \\ $$
Commented by Tinkutara last updated on 10/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
