Question Number 20054 by Tinkutara last updated on 21/Aug/17

$$\mathrm{If}\:\alpha\:\mathrm{and}\:\beta\:\left(\alpha\:<\:\beta\right)\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation}\:{x}^{\mathrm{2}} \:+\:{bx}\:+\:{c}\:=\:\mathrm{0},\:\mathrm{where} \\ $$$${c}\:<\:\mathrm{0}\:<\:{b},\:\mathrm{then} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{0}\:<\:\alpha\:<\:\beta \\ $$$$\left(\mathrm{2}\right)\:\alpha\:<\:\mathrm{0}\:<\:\beta\:<\:\mid\alpha\mid \\ $$$$\left(\mathrm{3}\right)\:\alpha\:<\:\beta\:<\:\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\alpha\:<\:\mathrm{0}\:<\:\mid\alpha\mid\:<\:\beta \\ $$
Answered by ajfour last updated on 21/Aug/17
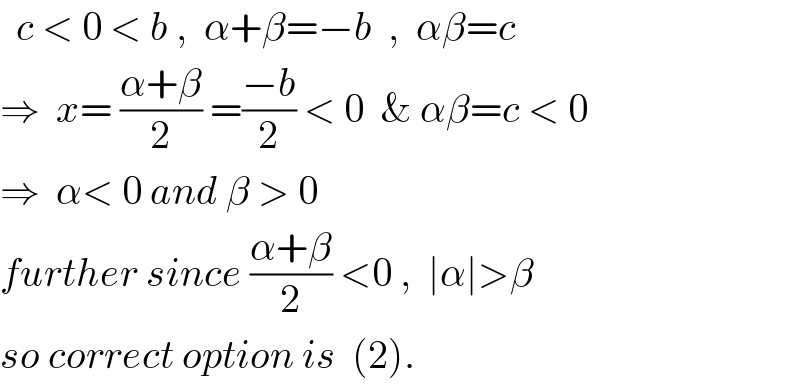
$$\:\:{c}\:<\:\mathrm{0}\:<\:{b}\:,\:\:\alpha+\beta=−{b}\:\:,\:\:\alpha\beta={c} \\ $$$$\Rightarrow\:\:{x}=\:\frac{\alpha+\beta}{\mathrm{2}}\:=\frac{−{b}}{\mathrm{2}}\:<\:\mathrm{0}\:\:\&\:\alpha\beta={c}\:<\:\mathrm{0} \\ $$$$\Rightarrow\:\:\alpha<\:\mathrm{0}\:{and}\:\beta\:>\:\mathrm{0} \\ $$$${further}\:{since}\:\frac{\alpha+\beta}{\mathrm{2}}\:<\mathrm{0}\:,\:\:\mid\alpha\mid>\beta \\ $$$${so}\:{correct}\:{option}\:{is}\:\:\left(\mathrm{2}\right). \\ $$
Commented by Tinkutara last updated on 21/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
