Menu Close

If-are-the-three-roots-of-the-3x-3-12x-2-77x-11-0-find-the-value-of-1-1-1-

Tinku Tara 0 Comments
Pin




Question Number 119408 by ZiYangLee last updated on 24/Oct/20
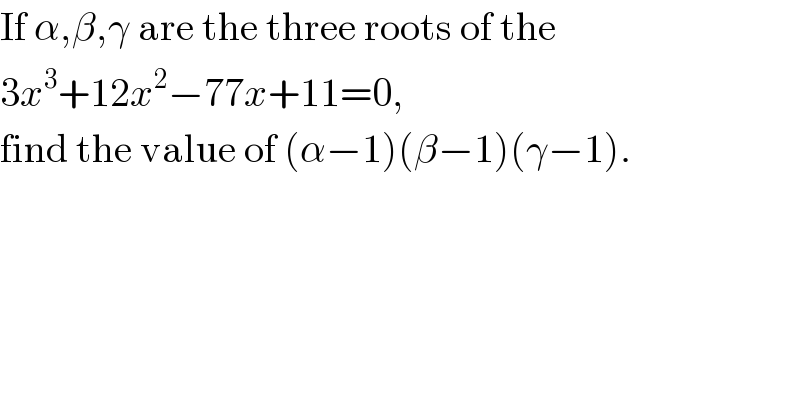
If α,β,γ are the three roots of the 3x^3 +12x^2 −77x+11=0, find the value of (α−1)(β−1)(γ−1).
$$\mathrm{If}\:\alpha,\beta,\gamma\:\mathrm{are}\:\mathrm{the}\:\mathrm{three}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{3}{x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} −\mathrm{77}{x}+\mathrm{11}=\mathrm{0}, \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\left(\alpha−\mathrm{1}\right)\left(\beta−\mathrm{1}\right)\left(\gamma−\mathrm{1}\right). \\ $$
Commented by liberty last updated on 24/Oct/20
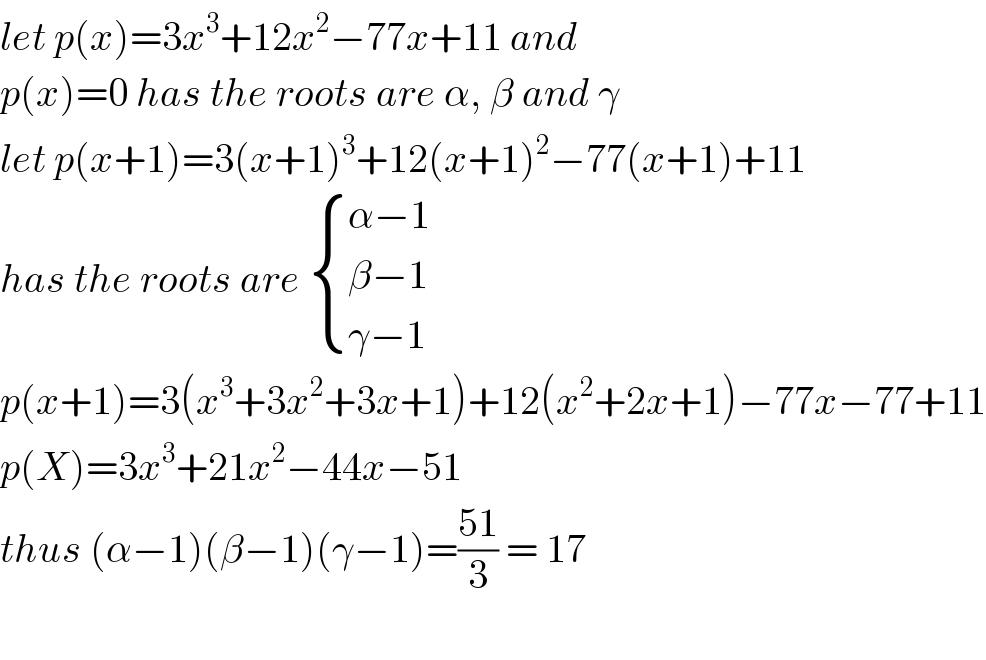
let p(x)=3x^3 +12x^2 −77x+11 and p(x)=0 has the roots are α, β and γ let p(x+1)=3(x+1)^3 +12(x+1)^2 −77(x+1)+11 has the roots are { ((α−1)),((β−1)),((γ−1)) :} p(x+1)=3(x^3 +3x^2 +3x+1)+12(x^2 +2x+1)−77x−77+11 p(X)=3x^3 +21x^2 −44x−51 thus (α−1)(β−1)(γ−1)=((51)/3) = 17
$${let}\:{p}\left({x}\right)=\mathrm{3}{x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} −\mathrm{77}{x}+\mathrm{11}\:{and} \\ $$$${p}\left({x}\right)=\mathrm{0}\:{has}\:{the}\:{roots}\:{are}\:\alpha,\:\beta\:{and}\:\gamma \\ $$$${let}\:{p}\left({x}+\mathrm{1}\right)=\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{3}} +\mathrm{12}\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{77}\left({x}+\mathrm{1}\right)+\mathrm{11} \\ $$$${has}\:{the}\:{roots}\:{are}\:\begin{cases}{\alpha−\mathrm{1}}\\{\beta−\mathrm{1}}\\{\gamma−\mathrm{1}}\end{cases} \\ $$$${p}\left({x}+\mathrm{1}\right)=\mathrm{3}\left({x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)+\mathrm{12}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)−\mathrm{77}{x}−\mathrm{77}+\mathrm{11} \\ $$$${p}\left({X}\right)=\mathrm{3}{x}^{\mathrm{3}} +\mathrm{21}{x}^{\mathrm{2}} −\mathrm{44}{x}−\mathrm{51} \\ $$$${thus}\:\left(\alpha−\mathrm{1}\right)\left(\beta−\mathrm{1}\right)\left(\gamma−\mathrm{1}\right)=\frac{\mathrm{51}}{\mathrm{3}}\:=\:\mathrm{17} \\ $$$$ \\ $$
Answered by mr W last updated on 24/Oct/20
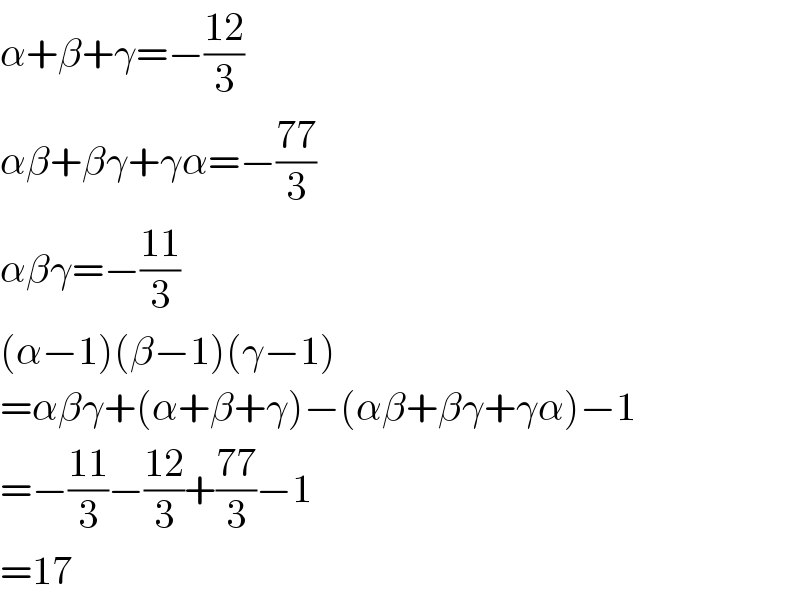
α+β+γ=−((12)/3) αβ+βγ+γα=−((77)/3) αβγ=−((11)/3) (α−1)(β−1)(γ−1) =αβγ+(α+β+γ)−(αβ+βγ+γα)−1 =−((11)/3)−((12)/3)+((77)/3)−1 =17
$$\alpha+\beta+\gamma=−\frac{\mathrm{12}}{\mathrm{3}} \\ $$$$\alpha\beta+\beta\gamma+\gamma\alpha=−\frac{\mathrm{77}}{\mathrm{3}} \\ $$$$\alpha\beta\gamma=−\frac{\mathrm{11}}{\mathrm{3}} \\ $$$$\left(\alpha−\mathrm{1}\right)\left(\beta−\mathrm{1}\right)\left(\gamma−\mathrm{1}\right) \\ $$$$=\alpha\beta\gamma+\left(\alpha+\beta+\gamma\right)−\left(\alpha\beta+\beta\gamma+\gamma\alpha\right)−\mathrm{1} \\ $$$$=−\frac{\mathrm{11}}{\mathrm{3}}−\frac{\mathrm{12}}{\mathrm{3}}+\frac{\mathrm{77}}{\mathrm{3}}−\mathrm{1} \\ $$$$=\mathrm{17} \\ $$
Commented by ZiYangLee last updated on 24/Oct/20
★★★
$$\bigstar\bigstar\bigstar \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *