Menu Close

If-at-a-height-of-40-m-the-direction-of-motion-of-a-projectile-makes-an-angle-pi-4-with-the-horizontal-then-its-initial-velocity-and-angle-of-projection-are-respectively-a-30-1-2-cos-1-4-5

Tinku Tara 0 Comments
Pin




Question Number 20316 by Tinkutara last updated on 25/Aug/17
If at a height of 40 m, the direction of motion of a projectile makes an angle π/4 with the horizontal, then its initial velocity and angle of projection are, respectively (a) 30, (1/2)cos^(−1) (−(4/5)) (b) 30, (1/2)cos^(−1) (−(1/2)) (c) 50, (1/2)cos^(−1) (−(8/(25))) (d) 60, (1/2)cos^(−1) (−(1/4))
$$\mathrm{If}\:\mathrm{at}\:\mathrm{a}\:\mathrm{height}\:\mathrm{of}\:\mathrm{40}\:\mathrm{m},\:\mathrm{the}\:\mathrm{direction}\:\mathrm{of} \\ $$$$\mathrm{motion}\:\mathrm{of}\:\mathrm{a}\:\mathrm{projectile}\:\mathrm{makes}\:\mathrm{an}\:\mathrm{angle} \\ $$$$\pi/\mathrm{4}\:\mathrm{with}\:\mathrm{the}\:\mathrm{horizontal},\:\mathrm{then}\:\mathrm{its}\:\mathrm{initial} \\ $$$$\mathrm{velocity}\:\mathrm{and}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{projection}\:\mathrm{are}, \\ $$$$\mathrm{respectively} \\ $$$$\left({a}\right)\:\mathrm{30},\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$$\left({b}\right)\:\mathrm{30},\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\left({c}\right)\:\mathrm{50},\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{8}}{\mathrm{25}}\right) \\ $$$$\left({d}\right)\:\mathrm{60},\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$
Commented by Tinkutara last updated on 25/Aug/17
I think velocity of projection should be given. Isn′t it?
$$\mathrm{I}\:\mathrm{think}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{projection}\:\mathrm{should}\:\mathrm{be} \\ $$$$\mathrm{given}.\:\mathrm{Isn}'\mathrm{t}\:\mathrm{it}? \\ $$
Commented by ajfour last updated on 25/Aug/17
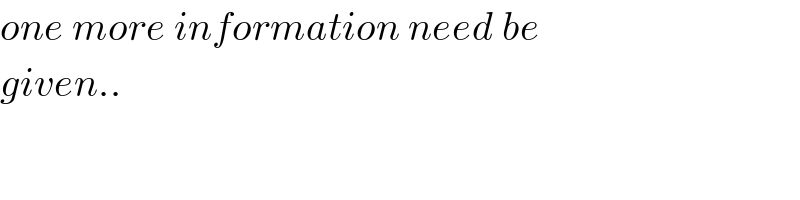
one more information need be given..
$${one}\:{more}\:{information}\:{need}\:{be} \\ $$$${given}.. \\ $$
Commented by Tinkutara last updated on 25/Aug/17
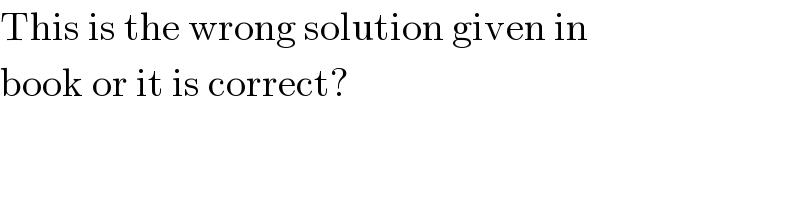
This is the wrong solution given in book or it is correct?
$$\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{wrong}\:\mathrm{solution}\:\mathrm{given}\:\mathrm{in} \\ $$$$\mathrm{book}\:\mathrm{or}\:\mathrm{it}\:\mathrm{is}\:\mathrm{correct}? \\ $$
Commented by Tinkutara last updated on 25/Aug/17
Commented by Joel577 last updated on 25/Aug/17
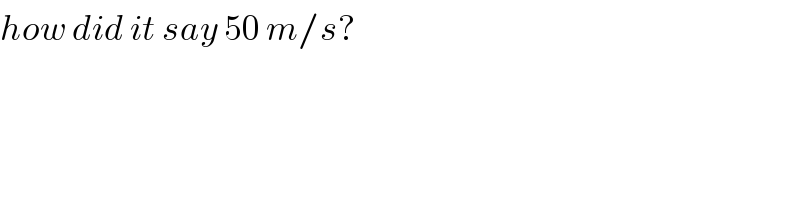
how did it say 50 m/s?
$${how}\:{did}\:{it}\:{say}\:\mathrm{50}\:{m}/{s}? \\ $$
Commented by Tinkutara last updated on 25/Aug/17
Yes, so this solution is wrong but it is in my book.
$$\mathrm{Yes},\:\mathrm{so}\:\mathrm{this}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{but}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{in}\:\mathrm{my}\:\mathrm{book}. \\ $$
Commented by ajfour last updated on 25/Aug/17
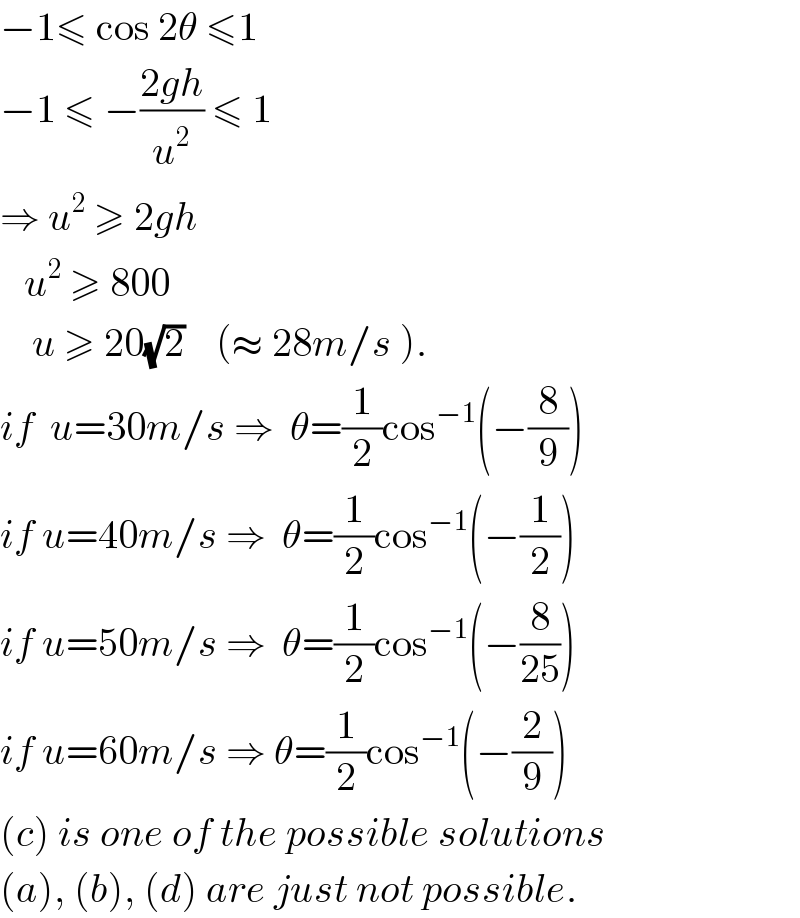
−1≤ cos 2θ ≤1 −1 ≤ −((2gh)/u^2 ) ≤ 1 ⇒ u^2 ≥ 2gh u^2 ≥ 800 u ≥ 20(√2) (≈ 28m/s ). if u=30m/s ⇒ θ=(1/2)cos^(−1) (−(8/9)) if u=40m/s ⇒ θ=(1/2)cos^(−1) (−(1/2)) if u=50m/s ⇒ θ=(1/2)cos^(−1) (−(8/(25))) if u=60m/s ⇒ θ=(1/2)cos^(−1) (−(2/9)) (c) is one of the possible solutions (a), (b), (d) are just not possible.
$$−\mathrm{1}\leqslant\:\mathrm{cos}\:\mathrm{2}\theta\:\leqslant\mathrm{1} \\ $$$$−\mathrm{1}\:\leqslant\:−\frac{\mathrm{2}{gh}}{{u}^{\mathrm{2}} }\:\leqslant\:\mathrm{1} \\ $$$$\Rightarrow\:{u}^{\mathrm{2}} \:\geqslant\:\mathrm{2}{gh}\:\: \\ $$$$\:\:\:{u}^{\mathrm{2}} \:\geqslant\:\mathrm{800} \\ $$$$\:\:\:\:{u}\:\geqslant\:\mathrm{20}\sqrt{\mathrm{2}}\:\:\:\:\left(\approx\:\mathrm{28}{m}/{s}\:\right). \\ $$$${if}\:\:{u}=\mathrm{30}{m}/{s}\:\Rightarrow\:\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{8}}{\mathrm{9}}\right) \\ $$$${if}\:{u}=\mathrm{40}{m}/{s}\:\Rightarrow\:\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${if}\:{u}=\mathrm{50}{m}/{s}\:\Rightarrow\:\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{8}}{\mathrm{25}}\right) \\ $$$${if}\:{u}=\mathrm{60}{m}/{s}\:\Rightarrow\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{2}}{\mathrm{9}}\right) \\ $$$$\left({c}\right)\:{is}\:{one}\:{of}\:{the}\:{possible}\:{solutions} \\ $$$$\left({a}\right),\:\left({b}\right),\:\left({d}\right)\:{are}\:{just}\:{not}\:{possible}. \\ $$
Commented by Tinkutara last updated on 25/Aug/17
Thanks you very much Sir! So it is to be seen by the options.
$$\mathrm{Thanks}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}!\:\mathrm{So}\:\mathrm{it}\:\mathrm{is}\:\mathrm{to} \\ $$$$\mathrm{be}\:\mathrm{seen}\:\mathrm{by}\:\mathrm{the}\:\mathrm{options}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *