Menu Close

If-ax-2-2hxy-by-2-1-show-that-d-2-y-dx-2-h-2-ab-hx-by-3-

Tinku Tara 0 Comments
Pin




Question Number 84236 by niroj last updated on 10/Mar/20
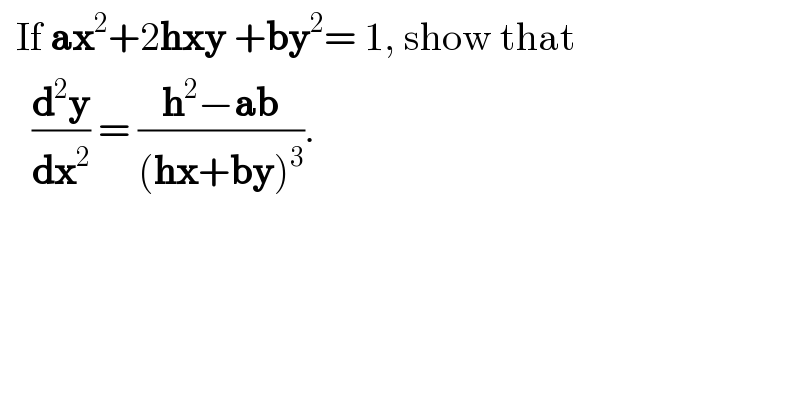
If ax^2 +2hxy +by^2 = 1, show that (d^2 y/dx^2 ) = ((h^2 −ab)/((hx+by)^3 )).
$$\:\:\mathrm{If}\:\boldsymbol{\mathrm{ax}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{hxy}}\:+\boldsymbol{\mathrm{by}}^{\mathrm{2}} =\:\mathrm{1},\:\mathrm{show}\:\mathrm{that} \\ $$$$\:\:\:\:\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}} }\:=\:\frac{\boldsymbol{\mathrm{h}}^{\mathrm{2}} −\boldsymbol{\mathrm{ab}}}{\left(\boldsymbol{\mathrm{hx}}+\boldsymbol{\mathrm{by}}\right)^{\mathrm{3}} }. \\ $$
Answered by TANMAY PANACEA last updated on 10/Mar/20
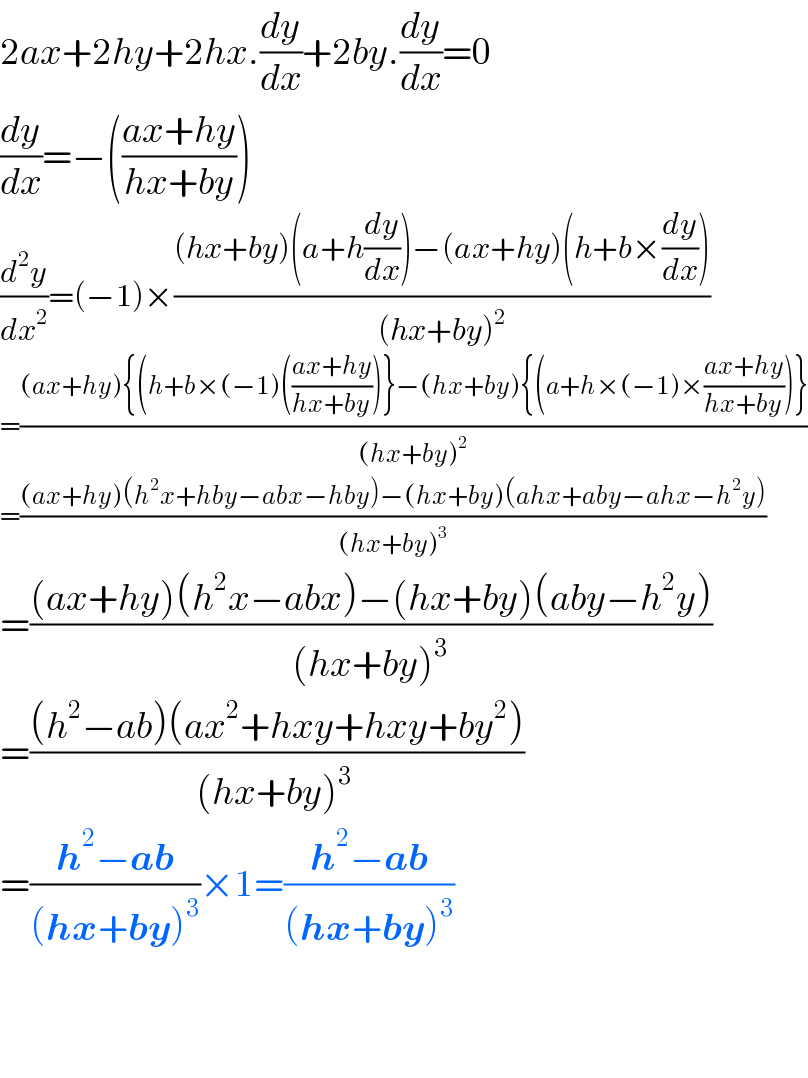
2ax+2hy+2hx.(dy/dx)+2by.(dy/dx)=0 (dy/dx)=−(((ax+hy)/(hx+by))) (d^2 y/dx^2 )=(−1)×(((hx+by)(a+h(dy/dx))−(ax+hy)(h+b×(dy/dx)))/((hx+by)^2 )) =(((ax+hy){(h+b×(−1)(((ax+hy)/(hx+by)))}−(hx+by){(a+h×(−1)×((ax+hy)/(hx+by)))})/((hx+by)^(2 ) )) =(((ax+hy)(h^2 x+hby−abx−hby)−(hx+by)(ahx+aby−ahx−h^2 y))/((hx+by)^3 )) =(((ax+hy)(h^2 x−abx)−(hx+by)(aby−h^2 y))/((hx+by)^3 )) =(((h^2 −ab)(ax^2 +hxy+hxy+by^2 ))/((hx+by)^(3 ) )) =((h^2 −ab)/((hx+by)^3 ))×1=((h^2 −ab)/((hx+by)^3 ))
$$\mathrm{2}{ax}+\mathrm{2}{hy}+\mathrm{2}{hx}.\frac{{dy}}{{dx}}+\mathrm{2}{by}.\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=−\left(\frac{{ax}+{hy}}{{hx}+{by}}\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\left(−\mathrm{1}\right)×\frac{\left({hx}+{by}\right)\left({a}+{h}\frac{{dy}}{{dx}}\right)−\left({ax}+{hy}\right)\left({h}+{b}×\frac{{dy}}{{dx}}\right)}{\left({hx}+{by}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left({ax}+{hy}\right)\left\{\left({h}+{b}×\left(−\mathrm{1}\right)\left(\frac{{ax}+{hy}}{{hx}+{by}}\right)\right\}−\left({hx}+{by}\right)\left\{\left({a}+{h}×\left(−\mathrm{1}\right)×\frac{{ax}+{hy}}{{hx}+{by}}\right)\right\}\right.}{\left({hx}+{by}\right)^{\mathrm{2}\:} } \\ $$$$=\frac{\left({ax}+{hy}\right)\left({h}^{\mathrm{2}} {x}+{hby}−{abx}−{hby}\right)−\left({hx}+{by}\right)\left({ahx}+{aby}−{ahx}−{h}^{\mathrm{2}} {y}\right)}{\left({hx}+{by}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left({ax}+{hy}\right)\left({h}^{\mathrm{2}} {x}−{abx}\right)−\left({hx}+{by}\right)\left({aby}−{h}^{\mathrm{2}} {y}\right)}{\left({hx}+{by}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left({h}^{\mathrm{2}} −{ab}\right)\left({ax}^{\mathrm{2}} +{hxy}+{hxy}+{by}^{\mathrm{2}} \right)}{\left({hx}+{by}\right)^{\mathrm{3}\:} } \\ $$$$=\frac{\boldsymbol{{h}}^{\mathrm{2}} −\boldsymbol{{ab}}}{\left(\boldsymbol{{hx}}+\boldsymbol{{by}}\right)^{\mathrm{3}} }×\mathrm{1}=\frac{\boldsymbol{{h}}^{\mathrm{2}} −\boldsymbol{{ab}}}{\left(\boldsymbol{{hx}}+\boldsymbol{{by}}\right)^{\mathrm{3}} } \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *