If-ax-2-bx-c-i-0-has-purely-imaginary-roots-where-a-b-c-are-non-zero-real-answer-given-a-b-2-c-I-think-question-is-wrong-since-if-z-1-and-z-2-are-roots-than-z-1-z-2-b-a-purely-imaginary-pu

Question Number 51843 by prakash jain last updated on 31/Dec/18

I f {a x}^{2} + b x + c + i = 0 has purely

imaginary roots where

a, b, c a r e n o n - z e r o r e a l .

a n s w e r g i v e n : a = b^{2} c

I think question is wrong

since if z_{1} and z_{2} are roots than

z_{1} + z_{2} = - \frac{b}{a}

p u r e l y i m a g i n a r y = p u r e l y r e a l

n o t p o s s i b l e

Can some point a mistake .

Commented by Rasheed.Sindhi last updated on 31/Dec/18

S i r P r a k a s h J a i n!

V e r y H a p p y t o s e e y o u a f t e r

l o n g t i m e o n t h i s p l a t f o r m!

I r e m e m b e r t h e p e r i o d l e d b y y o u

a n d Y o z z i o n t h i s p l a t f o r m! T h e

p e r i o d w h i c h w a s f u l l o f c o n c e p t u a l

d i s c u s s i o n s a n d t o p i c b a s e d l o n g s e s s i o n s!

Commented by Rasheed.Sindhi last updated on 31/Dec/18

M a y I b e s o l u c k y t o l e a r n m o r e f r o m

y o u!

Commented by prakash jain last updated on 03/Jan/19

Hi Rasheed, good to see you are still around. I am learning from you and everyone else in the forum.

Answered by ajfour last updated on 31/Dec/18

l e t x = i q

- {a q}^{2} + i b q + c + i = 0

\Rightarrow {a q}^{2} = c & b q + 1 = 0

\Rightarrow a = b^{2} c .

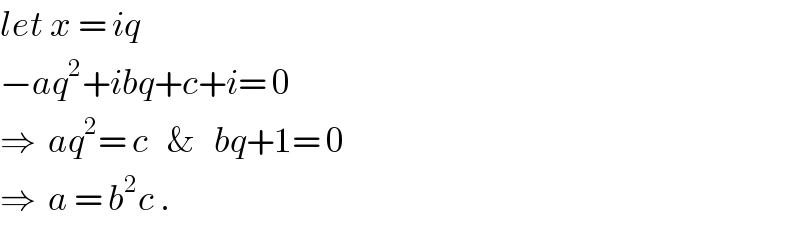
Commented by prakash jain last updated on 31/Dec/18

This is valid only when question says

one of the roots is imaginary .

a = b^{2} c

b^{2} {c x}^{2} + b x + c + i = 0

x^{2} + \frac{x}{b c} + \frac{c + i}{b^{2} c} = 0

clearly x = - \frac{i}{b} is a root as you

calculated .

let other root be z .

(x + \frac{i}{b}) (x - z) = 0

\frac{i}{b} - z = \frac{1}{b c} \Rightarrow z = \frac{i}{b} - \frac{1}{b c}

\frac{1}{b c} is real so other root is not

purely imaginary .