If-ax-2-by-2-2hxy-2gx-2fy-c-0-be-the-equation-of-an-ellipse-find-coordinates-of-center-of-ellipse-Q-45506-another-solution-

Question Number 45565 by ajfour last updated on 14/Oct/18

I f {a x}^{2} + {b y}^{2} + 2 h x y + 2 g x + 2 f y + c = 0

b e t h e e q u a t i o n o f a n e l l i p s e, f i n d

c o o r d i n a t e s o f c e n t e r o f e l l i p s e .

Q . 45506 (a n o t h e r s o l u t i o n)

Answered by ajfour last updated on 14/Oct/18

l e t c e n t r e o f e l l i p s e b e (p, q) .

I t s e q u a t i o n i n s t a n d a r d

o r i e n t a t i o n b e \frac{{(u - p)}^{2}}{A^{2}} + \frac{{(v - q)}^{2}}{B^{2}} = 1

w h e n r o t a t e d b y a n g l e ϕ,

l e t (u, v) \to (x, y)

u - p = (x - p) \cos ϕ + (y - q) \sin ϕ

v - q = (y - q) \cos ϕ - (x - p) \sin ϕ

T h e n

\frac{{[(x - p) \cos ϕ + (y - q) \sin ϕ]}^{2}}{A^{2}}

+ \frac{{[(y - q) \cos ϕ - (x - p) \sin ϕ]}^{2}}{B^{2}} - 1

= λ ({a x}^{2} + {b y}^{2} + 2 h x y + 2 g x + 2 f y + c)

(f o r a l l v a l u e s o f x a n d y; w h e t h e r

t h e e x p r e s s i o n s o n l . h . s . a n d r . h . s .

b e e q u a l t o z e r o o r n o t)

l e t \underline{y = q}, t h e n

{(x - p)}^{2} (\frac{\cos^{2} ϕ}{A^{2}} + \frac{\sin^{2} ϕ}{B^{2}})

= λ ({a x}^{2} + {b q}^{2} + 2 h q x + 2 g x + 2 f q + c)

\frac{c o e f f . o f x}{c o e f f . o f x^{2}} = \frac{- 2 p}{1} = \frac{2 (h q + g)}{a}

\Rightarrow a p + h q = - g \dots . (i)

s i m i l a r l y i f \underline{x = p}, t h e n

{(y - q)}^{2} (\frac{\sin^{2} ϕ}{A^{2}} + \frac{\cos^{2} ϕ}{B^{2}})

= λ ({a p}^{2} + {b y}^{2} + 2 h p y + 2 g p + 2 f y + c)

\frac{c o e f f . o f y}{c o e f f . o f y^{2}} = \frac{- 2 q}{1} = \frac{2 (h p + f)}{b}

\Rightarrow h p + b q = - f \dots . (i i)

N o w s o l v i n g (i) & (i i) f o r p, q

{\begin{cases} a p + h q = - g \\ h p + b q = - f \end{cases}

p = \frac{f h - b g}{a b - h^{2}}; q = \frac{g h - a f}{a b - h^{2}} .

Commented by ajfour last updated on 14/Oct/18

\frac{c o e f f . o f x y}{c o e f f . o f x^{2} - c o e f f . o f y^{2}}

= \frac{2 \sin ϕ \cos ϕ (\frac{1}{A^{2}} - \frac{1}{B^{2}})}{(\cos^{2} ϕ - \sin^{2} ϕ) (\frac{1}{A^{2}} - \frac{1}{B^{2}})}

= \frac{2 h}{a - b}

\Rightarrow \tan 2 ϕ = \frac{2 h}{a - b} .

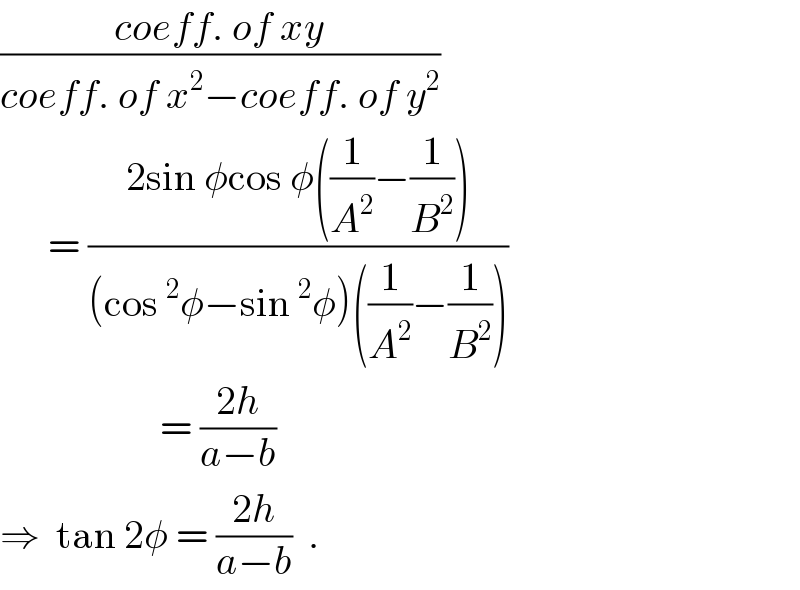
Commented by MrW3 last updated on 14/Oct/18

t h a n k s a l o t s i r!

Answered by MJS last updated on 14/Oct/18

solving the given equation for x and y

x = - \frac{h y + g}{a} \pm \sqrt{\dots}

y = - \frac{h x + f}{b} \pm \sqrt{\dots}

x = - \frac{h y + g}{a} \land y = - \frac{h x + f}{b} \Rightarrow

\Rightarrow x = \frac{f h - b g}{a b - h^{2}} \land y = \frac{g h - a f}{a b - h^{2}}

no matter what kind of conic the equation is,

the center is (\begin{matrix} \frac{f h - b g}{a b - h^{2}} \\ \frac{g h - a f}{a b - h^{2}} \end{matrix})

Commented by ajfour last updated on 14/Oct/18

t h a n k s f o r t h e s i m p l e w a y s i r .

Commented by MrW3 last updated on 14/Oct/18

t h a n k s a l o t s i r!

Commented by MJS last updated on 14/Oct/18

{you}^{'} re welcome

Facebook Tweet Pin