Menu Close

If-ax-2-by-2-2hxy-2gx-2fy-c-0-be-the-equation-of-an-ellipse-find-coordinates-of-its-centre-

Tinku Tara 0 Comments
Pin




Question Number 45506 by ajfour last updated on 13/Oct/18
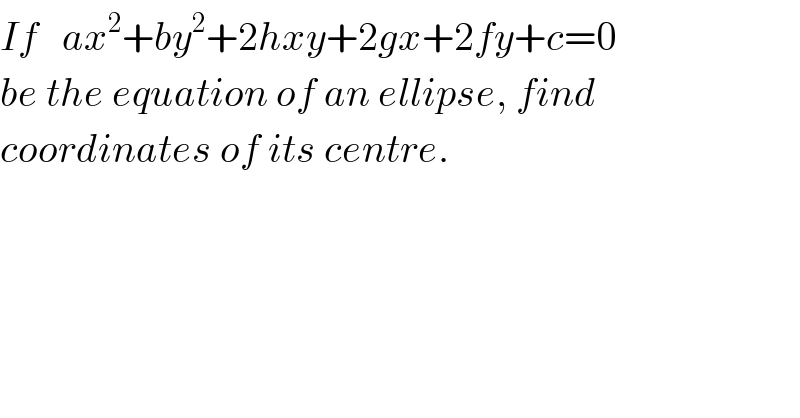
If ax^2 +by^2 +2hxy+2gx+2fy+c=0 be the equation of an ellipse, find coordinates of its centre.
$${If}\:\:\:{ax}^{\mathrm{2}} +{by}^{\mathrm{2}} +\mathrm{2}{hxy}+\mathrm{2}{gx}+\mathrm{2}{fy}+{c}=\mathrm{0} \\ $$$${be}\:{the}\:{equation}\:{of}\:{an}\:{ellipse},\:{find} \\ $$$${coordinates}\:{of}\:{its}\:{centre}. \\ $$
Answered by MrW3 last updated on 14/Oct/18
let θ=rotation angle of ellipse and (p,q)=center of ellipse eqn. of ellipse in uv−system is (u^2 /U^2 )+(v^2 /V^2 )=1 x=u cos θ−v sin θ+p y=u sin θ+v cos θ+q ax^2 =a cos^2 θ u^2 +a sin^2 θ v^2 −a sin 2θ uv+2ap cos θ u−2ap sin θ v+ap^2 by^2 =b sin^2 θ u^2 +b cos^2 θ v^2 +b sin 2θ uv+2bq sin θ u+2bq cos θ v+bq^2 2hxy=h sin 2θ u^2 −h sin 2θ v^2 +2h cos 2θ uv+2h(p sin θ+q cos θ) u+2h(p cos θ−q sin θ)v+2hpq 2gx=2g cos θ u−2g sin θ v+2gp 2fy=2f sin θ u+2f cos θ v+2fq+c term u^2 = A=a cos^2 θ+b sin^2 θ+h sin 2θ term v^2 = B=a sin^2 θ+b cos^2 θ−h sin 2θ term uv=C=−(a−b) sin 2θ+2h cos 2θ term u=D=2ap cos θ+2bq sin θ+2h(p sin θ+q cos θ)+2g cos θ+2f sin θ term v=E=−2ap sin θ+2bq cos θ+2h(p cos θ−q sin θ)−2g sin θ+2f cos θ term const=F=ap^2 +bq^2 +2hpq+2gp+2fq (u^2 /U^2 )+(v^2 /V^2 )−1=0 C=−a sin 2θ+b sin 2θ+2h cos 2θ=0 ⇒tan 2θ=((2h)/(a−b))⇒θ=(1/2)tan^(−1) ((2h)/(a−b)) D=2ap cos θ+2bq sin θ+2h(p sin θ+q cos θ)+2g cos θ+2f sin θ=0 ⇒(a cos θ+h sin θ)p+(b sin θ+h cos θ)q+(g cos θ+f sin θ)=0 E=−2ap sin θ+2bq cos θ+2h(p cos θ−q sin θ)−2g sin θ+2f cos θ=0 ⇒(−a sin θ+h cos θ)p+(b cos θ−h sin θ)q−g sin θ+f cos θ=0 {(a cos θ+h sin θ)(b cos θ−h sin θ)−(−a sin θ+h cos θ)(b sin θ+h cos θ)}p+{(g cos θ+f sin θ)(b cos θ−h sin θ)−(−g sin θ+f cos θ)(b sin θ+h cos θ)}=0 {(ab cos^2 θ+((bh)/2) sin 2θ−((ah)/2) sin 2θ−h^2 sin^2 θ)−(−ab sin^2 θ+((bh)/2) sin 2θ−((ah)/2) sin 2θ+h^2 cos^2 θ)}p+{(bg cos^2 θ+((bf)/2) sin 2θ−((gh)/2) sin 2θ−fh sin^2 θ)−(−bg sin^2 θ+((bf)/2) sin 2θ−((gh)/2) sin 2θ+fh cos^2 θ)}=0 (ab−h^2 )p+(bg−fh)=0 ⇒p=((fh−bg)/(ab−h^2 )) to be continued..
$${let}\:\theta={rotation}\:{angle}\:{of}\:{ellipse}\:{and} \\ $$$$\left({p},{q}\right)={center}\:{of}\:{ellipse} \\ $$$${eqn}.\:{of}\:{ellipse}\:{in}\:{uv}−{system}\:{is} \\ $$$$\frac{{u}^{\mathrm{2}} }{{U}^{\mathrm{2}} }+\frac{{v}^{\mathrm{2}} }{{V}^{\mathrm{2}} }=\mathrm{1} \\ $$$$ \\ $$$${x}={u}\:\mathrm{cos}\:\theta−{v}\:\mathrm{sin}\:\theta+{p} \\ $$$${y}={u}\:\mathrm{sin}\:\theta+{v}\:\mathrm{cos}\:\theta+{q} \\ $$$$ \\ $$$${ax}^{\mathrm{2}} ={a}\:\mathrm{cos}^{\mathrm{2}} \:\theta\:{u}^{\mathrm{2}} +{a}\:\mathrm{sin}^{\mathrm{2}} \:\theta\:{v}^{\mathrm{2}} −{a}\:\mathrm{sin}\:\mathrm{2}\theta\:{uv}+\mathrm{2}{ap}\:\mathrm{cos}\:\theta\:{u}−\mathrm{2}{ap}\:\mathrm{sin}\:\theta\:{v}+{ap}^{\mathrm{2}} \\ $$$${by}^{\mathrm{2}} ={b}\:\mathrm{sin}^{\mathrm{2}} \:\theta\:{u}^{\mathrm{2}} +{b}\:\mathrm{cos}^{\mathrm{2}} \:\theta\:{v}^{\mathrm{2}} +{b}\:\mathrm{sin}\:\mathrm{2}\theta\:{uv}+\mathrm{2}{bq}\:\mathrm{sin}\:\theta\:{u}+\mathrm{2}{bq}\:\mathrm{cos}\:\theta\:{v}+{bq}^{\mathrm{2}} \\ $$$$\mathrm{2}{hxy}={h}\:\mathrm{sin}\:\mathrm{2}\theta\:{u}^{\mathrm{2}} −{h}\:\mathrm{sin}\:\mathrm{2}\theta\:{v}^{\mathrm{2}} +\mathrm{2}{h}\:\mathrm{cos}\:\mathrm{2}\theta\:{uv}+\mathrm{2}{h}\left({p}\:\mathrm{sin}\:\theta+{q}\:\mathrm{cos}\:\theta\right)\:{u}+\mathrm{2}{h}\left({p}\:\mathrm{cos}\:\theta−{q}\:\mathrm{sin}\:\theta\right){v}+\mathrm{2}{hpq} \\ $$$$\mathrm{2}{gx}=\mathrm{2}{g}\:\mathrm{cos}\:\theta\:{u}−\mathrm{2}{g}\:\mathrm{sin}\:\theta\:{v}+\mathrm{2}{gp} \\ $$$$\mathrm{2}{fy}=\mathrm{2}{f}\:\mathrm{sin}\:\theta\:{u}+\mathrm{2}{f}\:\mathrm{cos}\:\theta\:{v}+\mathrm{2}{fq}+{c} \\ $$$$ \\ $$$${term}\:{u}^{\mathrm{2}} =\:{A}={a}\:\mathrm{cos}^{\mathrm{2}} \:\theta+{b}\:\mathrm{sin}^{\mathrm{2}} \:\theta+{h}\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$${term}\:{v}^{\mathrm{2}} =\:{B}={a}\:\mathrm{sin}^{\mathrm{2}} \:\theta+{b}\:\mathrm{cos}^{\mathrm{2}} \:\theta−{h}\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$${term}\:{uv}={C}=−\left({a}−{b}\right)\:\mathrm{sin}\:\mathrm{2}\theta+\mathrm{2}{h}\:\mathrm{cos}\:\mathrm{2}\theta \\ $$$${term}\:{u}={D}=\mathrm{2}{ap}\:\mathrm{cos}\:\theta+\mathrm{2}{bq}\:\mathrm{sin}\:\theta+\mathrm{2}{h}\left({p}\:\mathrm{sin}\:\theta+{q}\:\mathrm{cos}\:\theta\right)+\mathrm{2}{g}\:\mathrm{cos}\:\theta+\mathrm{2}{f}\:\mathrm{sin}\:\theta \\ $$$${term}\:{v}={E}=−\mathrm{2}{ap}\:\mathrm{sin}\:\theta+\mathrm{2}{bq}\:\mathrm{cos}\:\theta+\mathrm{2}{h}\left({p}\:\mathrm{cos}\:\theta−{q}\:\mathrm{sin}\:\theta\right)−\mathrm{2}{g}\:\mathrm{sin}\:\theta+\mathrm{2}{f}\:\mathrm{cos}\:\theta \\ $$$${term}\:{const}={F}={ap}^{\mathrm{2}} +{bq}^{\mathrm{2}} +\mathrm{2}{hpq}+\mathrm{2}{gp}+\mathrm{2}{fq} \\ $$$$ \\ $$$$\frac{{u}^{\mathrm{2}} }{{U}^{\mathrm{2}} }+\frac{{v}^{\mathrm{2}} }{{V}^{\mathrm{2}} }−\mathrm{1}=\mathrm{0} \\ $$$${C}=−{a}\:\mathrm{sin}\:\mathrm{2}\theta+{b}\:\mathrm{sin}\:\mathrm{2}\theta+\mathrm{2}{h}\:\mathrm{cos}\:\mathrm{2}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{2}\theta=\frac{\mathrm{2}{h}}{{a}−{b}}\Rightarrow\theta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}{h}}{{a}−{b}} \\ $$$$ \\ $$$${D}=\mathrm{2}{ap}\:\mathrm{cos}\:\theta+\mathrm{2}{bq}\:\mathrm{sin}\:\theta+\mathrm{2}{h}\left({p}\:\mathrm{sin}\:\theta+{q}\:\mathrm{cos}\:\theta\right)+\mathrm{2}{g}\:\mathrm{cos}\:\theta+\mathrm{2}{f}\:\mathrm{sin}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\left({a}\:\mathrm{cos}\:\theta+{h}\:\mathrm{sin}\:\theta\right){p}+\left({b}\:\mathrm{sin}\:\theta+{h}\:\mathrm{cos}\:\theta\right){q}+\left({g}\:\mathrm{cos}\:\theta+{f}\:\mathrm{sin}\:\theta\right)=\mathrm{0} \\ $$$${E}=−\mathrm{2}{ap}\:\mathrm{sin}\:\theta+\mathrm{2}{bq}\:\mathrm{cos}\:\theta+\mathrm{2}{h}\left({p}\:\mathrm{cos}\:\theta−{q}\:\mathrm{sin}\:\theta\right)−\mathrm{2}{g}\:\mathrm{sin}\:\theta+\mathrm{2}{f}\:\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\left(−{a}\:\mathrm{sin}\:\theta+{h}\:\mathrm{cos}\:\theta\right){p}+\left({b}\:\mathrm{cos}\:\theta−{h}\:\mathrm{sin}\:\theta\right){q}−{g}\:\mathrm{sin}\:\theta+{f}\:\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$ \\ $$$$\left\{\left({a}\:\mathrm{cos}\:\theta+{h}\:\mathrm{sin}\:\theta\right)\left({b}\:\mathrm{cos}\:\theta−{h}\:\mathrm{sin}\:\theta\right)−\left(−{a}\:\mathrm{sin}\:\theta+{h}\:\mathrm{cos}\:\theta\right)\left({b}\:\mathrm{sin}\:\theta+{h}\:\mathrm{cos}\:\theta\right)\right\}{p}+\left\{\left({g}\:\mathrm{cos}\:\theta+{f}\:\mathrm{sin}\:\theta\right)\left({b}\:\mathrm{cos}\:\theta−{h}\:\mathrm{sin}\:\theta\right)−\left(−{g}\:\mathrm{sin}\:\theta+{f}\:\mathrm{cos}\:\theta\right)\left({b}\:\mathrm{sin}\:\theta+{h}\:\mathrm{cos}\:\theta\right)\right\}=\mathrm{0} \\ $$$$\left\{\left({ab}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\frac{{bh}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta−\frac{{ah}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta−{h}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta\right)−\left(−{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\frac{{bh}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta−\frac{{ah}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta+{h}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta\right)\right\}{p}+\left\{\left({bg}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\frac{{bf}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta−\frac{{gh}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta−{fh}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)−\left(−{bg}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\frac{{bf}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta−\frac{{gh}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta+{fh}\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)\right\}=\mathrm{0} \\ $$$$\left({ab}−{h}^{\mathrm{2}} \right){p}+\left({bg}−{fh}\right)=\mathrm{0} \\ $$$$\Rightarrow{p}=\frac{{fh}−{bg}}{{ab}−{h}^{\mathrm{2}} } \\ $$$${to}\:{be}\:{continued}.. \\ $$
Commented by MrW3 last updated on 14/Oct/18
continue... {(b sin θ+h cos θ)(−a sin θ+h cos θ)−(b cos θ−h sin θ)(a cos θ+h sin θ)}q+{(g cos θ+f sin θ)(−a sin θ+h cos θ)−(−g sin θ+f cos θ)(a cos θ+h sin θ)}=0 (h^2 −ab)q+(gh−af)=0 ⇒p=((fh−bg)/(ab−h^2 )) ⇒q=((gh−af)/(ab−h^2 )) ⇒θ=(1/2)tan^(−1) ((2h)/(a−b)) A=a cos^2 θ+b sin^2 θ+h sin 2θ B=a sin^2 θ+b cos^2 θ−h sin 2θ F=ap^2 +bq^2 +2hpq+2gp+2fq+c major and minor axis of ellipse: U=(√(−(F/A))) V=(√(−(F/B)))
$${continue}… \\ $$$$ \\ $$$$\left\{\left({b}\:\mathrm{sin}\:\theta+{h}\:\mathrm{cos}\:\theta\right)\left(−{a}\:\mathrm{sin}\:\theta+{h}\:\mathrm{cos}\:\theta\right)−\left({b}\:\mathrm{cos}\:\theta−{h}\:\mathrm{sin}\:\theta\right)\left({a}\:\mathrm{cos}\:\theta+{h}\:\mathrm{sin}\:\theta\right)\right\}{q}+\left\{\left({g}\:\mathrm{cos}\:\theta+{f}\:\mathrm{sin}\:\theta\right)\left(−{a}\:\mathrm{sin}\:\theta+{h}\:\mathrm{cos}\:\theta\right)−\left(−{g}\:\mathrm{sin}\:\theta+{f}\:\mathrm{cos}\:\theta\right)\left({a}\:\mathrm{cos}\:\theta+{h}\:\mathrm{sin}\:\theta\right)\right\}=\mathrm{0} \\ $$$$\left({h}^{\mathrm{2}} −{ab}\right){q}+\left({gh}−{af}\right)=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{p}=\frac{{fh}−{bg}}{{ab}−{h}^{\mathrm{2}} } \\ $$$$\Rightarrow{q}=\frac{{gh}−{af}}{{ab}−{h}^{\mathrm{2}} } \\ $$$$\Rightarrow\theta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}{h}}{{a}−{b}} \\ $$$$ \\ $$$${A}={a}\:\mathrm{cos}^{\mathrm{2}} \:\theta+{b}\:\mathrm{sin}^{\mathrm{2}} \:\theta+{h}\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$${B}={a}\:\mathrm{sin}^{\mathrm{2}} \:\theta+{b}\:\mathrm{cos}^{\mathrm{2}} \:\theta−{h}\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$${F}={ap}^{\mathrm{2}} +{bq}^{\mathrm{2}} +\mathrm{2}{hpq}+\mathrm{2}{gp}+\mathrm{2}{fq}+{c} \\ $$$$ \\ $$$${major}\:{and}\:{minor}\:{axis}\:{of}\:{ellipse}: \\ $$$${U}=\sqrt{−\frac{{F}}{{A}}} \\ $$$${V}=\sqrt{−\frac{{F}}{{B}}} \\ $$
Commented by ajfour last updated on 14/Oct/18
Thank you Sir, i believe it can be found some other way too, let me try..
$${Thank}\:{you}\:{Sir},\:{i}\:{believe}\:{it}\:{can} \\ $$$${be}\:{found}\:{some}\:{other}\:{way}\:{too},\:{let} \\ $$$${me}\:{try}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *