Question Number 56335 by Tawa1 last updated on 14/Mar/19
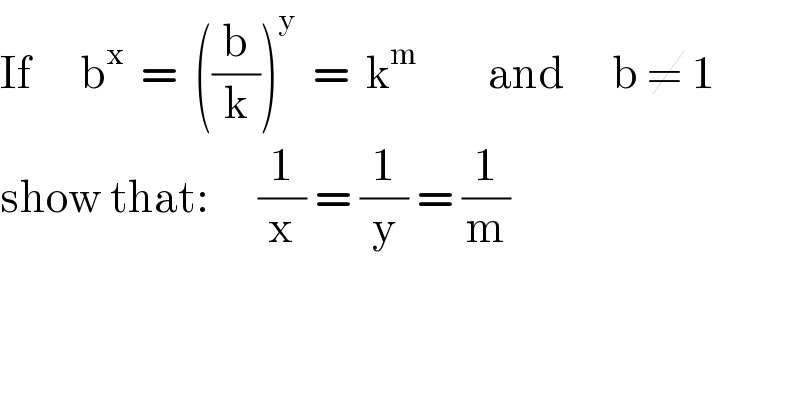
$$\mathrm{If}\:\:\:\:\:\:\mathrm{b}^{\mathrm{x}} \:\:=\:\:\left(\frac{\mathrm{b}}{\mathrm{k}}\right)^{\mathrm{y}} \:\:=\:\:\mathrm{k}^{\mathrm{m}} \:\:\:\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\:\mathrm{b}\:\neq\:\mathrm{1} \\ $$$$\mathrm{show}\:\mathrm{that}:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{y}}\:=\:\frac{\mathrm{1}}{\mathrm{m}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Mar/19
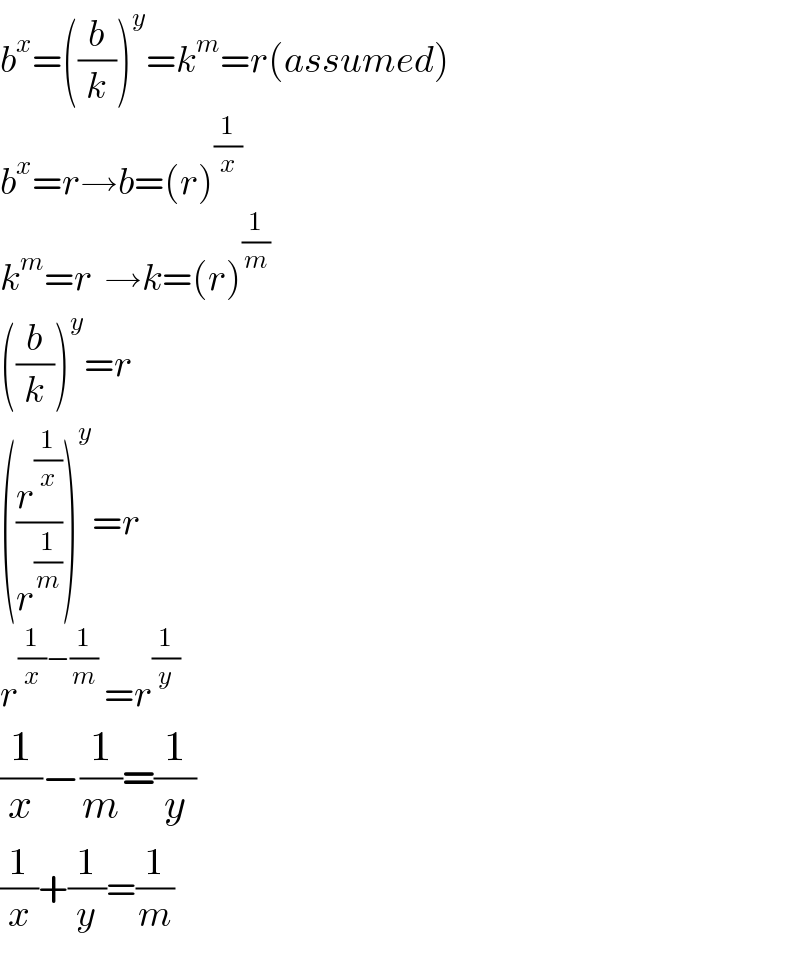
$${b}^{{x}} =\left(\frac{{b}}{{k}}\right)^{{y}} ={k}^{{m}} ={r}\left({assumed}\right) \\ $$$${b}^{{x}} ={r}\rightarrow{b}=\left({r}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$${k}^{{m}} ={r}\:\:\rightarrow{k}=\left({r}\right)^{\frac{\mathrm{1}}{{m}}} \\ $$$$\left(\frac{{b}}{{k}}\right)^{{y}} ={r} \\ $$$$\left(\frac{{r}^{\frac{\mathrm{1}}{{x}}} }{{r}^{\frac{\mathrm{1}}{{m}}} }\right)^{{y}} ={r} \\ $$$${r}^{\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{m}}} \:={r}^{\frac{\mathrm{1}}{{y}}} \\ $$$$\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{m}}=\frac{\mathrm{1}}{{y}} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{1}}{{m}}\:\:\: \\ $$
Commented by Tawa1 last updated on 14/Mar/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by $@ty@m last updated on 30/Mar/19
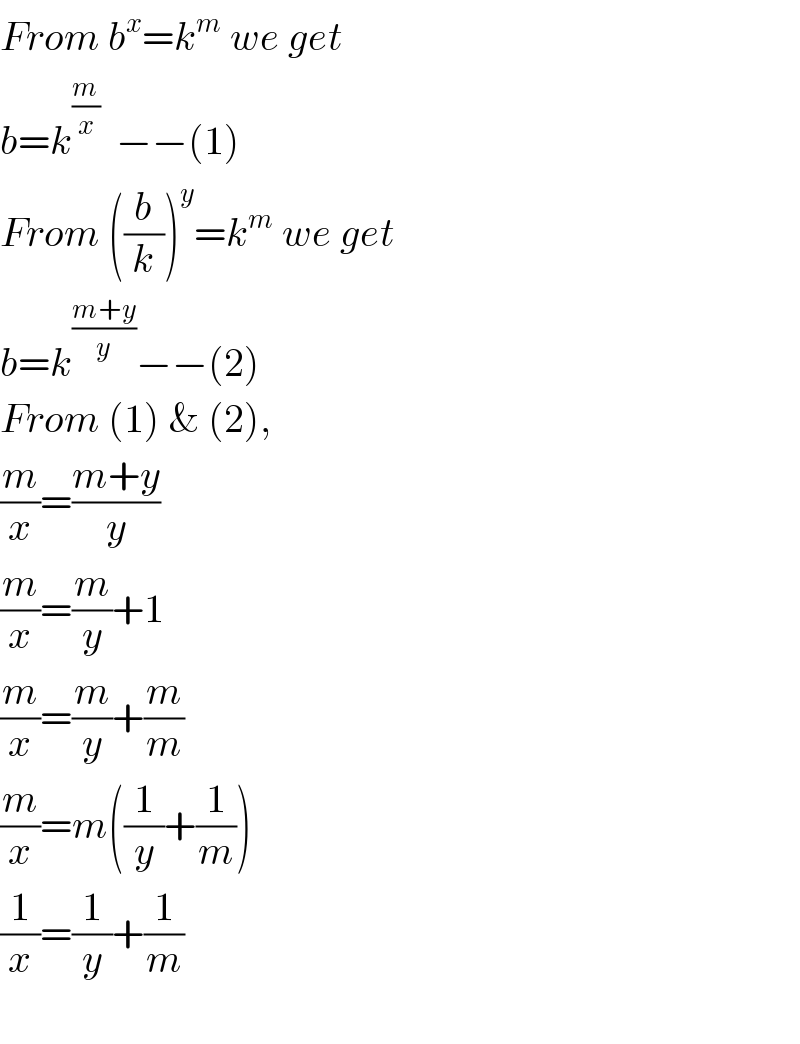
$${From}\:{b}^{{x}} ={k}^{{m}} \:{we}\:{get} \\ $$$${b}={k}^{\frac{{m}}{{x}}} \:\:−−\left(\mathrm{1}\right) \\ $$$${From}\:\left(\frac{{b}}{{k}}\right)^{{y}} ={k}^{{m}} \:{we}\:{get} \\ $$$${b}={k}^{\frac{{m}+{y}}{{y}}} −−\left(\mathrm{2}\right) \\ $$$${From}\:\left(\mathrm{1}\right)\:\&\:\left(\mathrm{2}\right), \\ $$$$\frac{{m}}{{x}}=\frac{{m}+{y}}{{y}} \\ $$$$\frac{{m}}{{x}}=\frac{{m}}{{y}}+\mathrm{1} \\ $$$$\frac{{m}}{{x}}=\frac{{m}}{{y}}+\frac{{m}}{{m}} \\ $$$$\frac{{m}}{{x}}={m}\left(\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{m}}\right) \\ $$$$\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{m}} \\ $$$$ \\ $$
