Question Number 35654 by chakraborty ankit last updated on 21/May/18
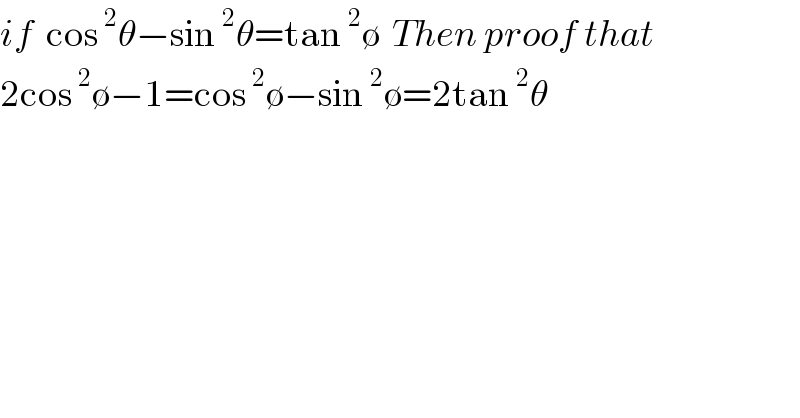
$${if}\:\:\mathrm{cos}\:^{\mathrm{2}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta=\mathrm{tan}\:^{\mathrm{2}} \emptyset\:\:{Then}\:{proof}\:{that} \\ $$$$\mathrm{2cos}\:^{\mathrm{2}} \emptyset−\mathrm{1}=\mathrm{cos}\:^{\mathrm{2}} \emptyset−\mathrm{sin}\:^{\mathrm{2}} \emptyset=\mathrm{2tan}\:^{\mathrm{2}} \theta \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/May/18
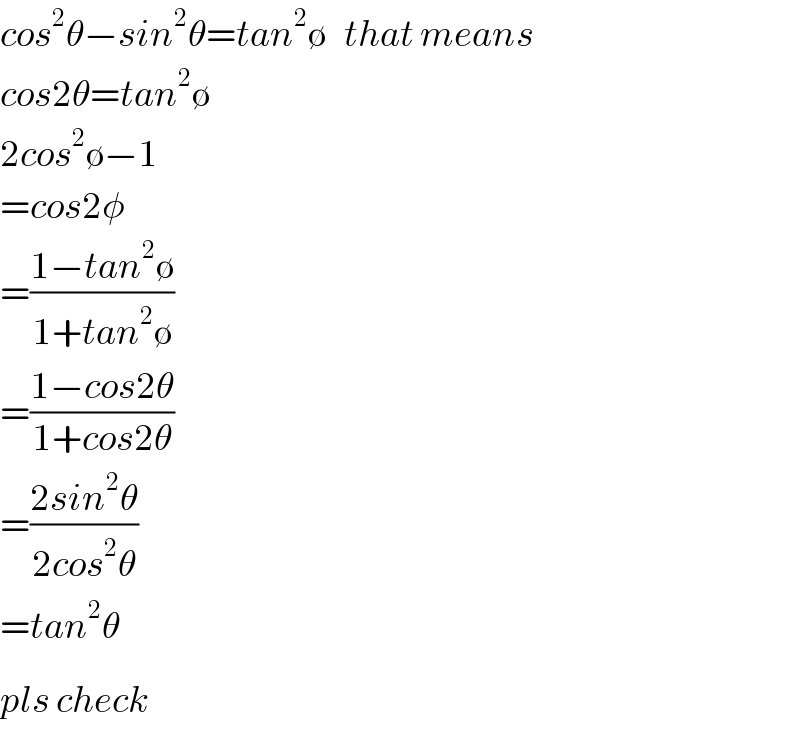
$${cos}^{\mathrm{2}} \theta−{sin}^{\mathrm{2}} \theta={tan}^{\mathrm{2}} \emptyset\:\:\:{that}\:{means} \\ $$$${cos}\mathrm{2}\theta={tan}^{\mathrm{2}} \emptyset \\ $$$$\mathrm{2}{cos}^{\mathrm{2}} \emptyset−\mathrm{1} \\ $$$$={cos}\mathrm{2}\phi \\ $$$$=\frac{\mathrm{1}−{tan}^{\mathrm{2}} \emptyset}{\mathrm{1}+{tan}^{\mathrm{2}} \emptyset} \\ $$$$=\frac{\mathrm{1}−{cos}\mathrm{2}\theta}{\mathrm{1}+{cos}\mathrm{2}\theta} \\ $$$$=\frac{\mathrm{2}{sin}^{\mathrm{2}} \theta}{\mathrm{2}{cos}^{\mathrm{2}} \theta} \\ $$$$={tan}^{\mathrm{2}} \theta \\ $$$${pls}\:{chec}\overset{} {{k}} \\ $$
