Question Number 50705 by 786786AM last updated on 19/Dec/18
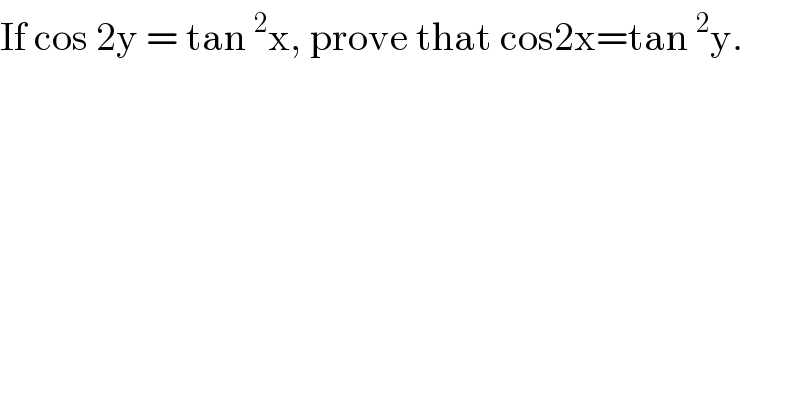
$$\mathrm{If}\:\mathrm{cos}\:\mathrm{2y}\:=\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{x},\:\mathrm{prove}\:\mathrm{that}\:\mathrm{cos2x}=\mathrm{tan}\:^{\mathrm{2}} \mathrm{y}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Dec/18

$${cos}\mathrm{2}{x} \\ $$$$=\frac{\mathrm{1}−{tan}^{\mathrm{2}} {x}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}} \\ $$$$=\frac{\mathrm{1}−{cos}\mathrm{2}{y}}{\mathrm{1}+{cos}\mathrm{2}{y}} \\ $$$$=\frac{\mathrm{2}{sin}^{\mathrm{2}} {y}}{\mathrm{2}{cos}^{\mathrm{2}} {y}} \\ $$$$={tan}^{\mathrm{2}} {y} \\ $$
