if-cos-3-x-cos-3-x-0-find-sin-2x-cos-2x-

Question Number 81170 by jagoll last updated on 10/Feb/20

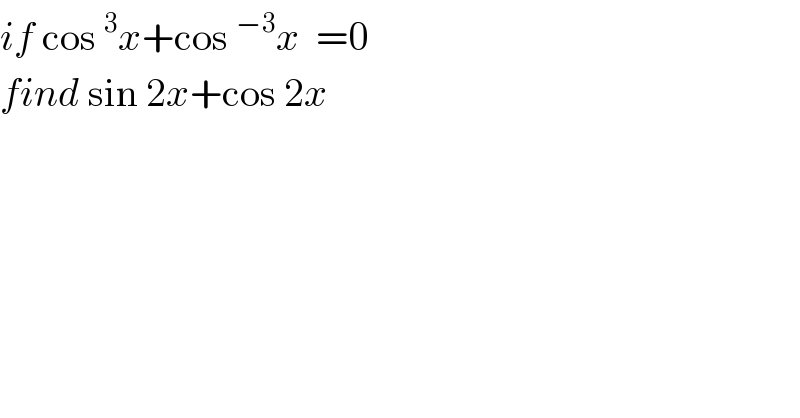
$${if}\:\mathrm{cos}\:^{\mathrm{3}} {x}+\mathrm{cos}\:^{−\mathrm{3}} {x}\:\:=\mathrm{0} \\ $$$${find}\:\mathrm{sin}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{2}{x} \\ $$

Commented by jagoll last updated on 10/Feb/20

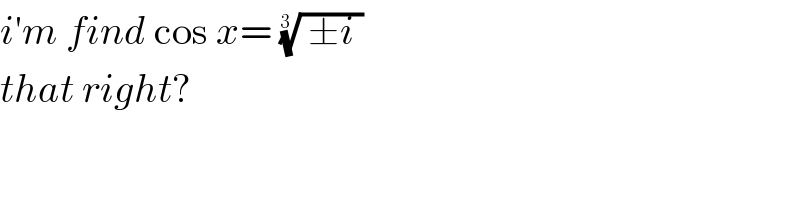
i′m find cos x= (( ±i ))^(1/(3 )) that right?

$${i}'{m}\:{find}\:\mathrm{cos}\:{x}=\:\sqrt[{\mathrm{3}\:}]{\:\pm{i}\:} \\ $$$${that}\:{right}? \\ $$

Commented by mr W last updated on 10/Feb/20

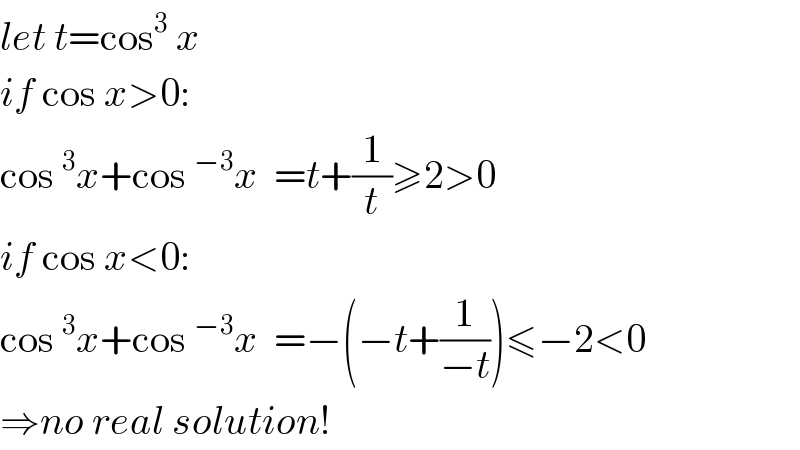
let t=cos^3 x if cos x>0: cos^3 x+cos^(−3) x =t+(1/t)≥2>0 if cos x<0: cos^3 x+cos^(−3) x =−(−t+(1/(−t)))≤−2<0 ⇒no real solution!

$${let}\:{t}=\mathrm{cos}^{\mathrm{3}} \:{x} \\ $$$${if}\:\mathrm{cos}\:{x}>\mathrm{0}: \\ $$$$\mathrm{cos}\:^{\mathrm{3}} {x}+\mathrm{cos}\:^{−\mathrm{3}} {x}\:\:={t}+\frac{\mathrm{1}}{{t}}\geqslant\mathrm{2}>\mathrm{0} \\ $$$${if}\:\mathrm{cos}\:{x}<\mathrm{0}: \\ $$$$\mathrm{cos}\:^{\mathrm{3}} {x}+\mathrm{cos}\:^{−\mathrm{3}} {x}\:\:=−\left(−{t}+\frac{\mathrm{1}}{−{t}}\right)\leqslant−\mathrm{2}<\mathrm{0} \\ $$$$\Rightarrow{no}\:{real}\:{solution}! \\ $$

Commented by jagoll last updated on 10/Feb/20

$${thank}\:{you}\:{sir} \\ $$

Commented by mr W last updated on 10/Feb/20

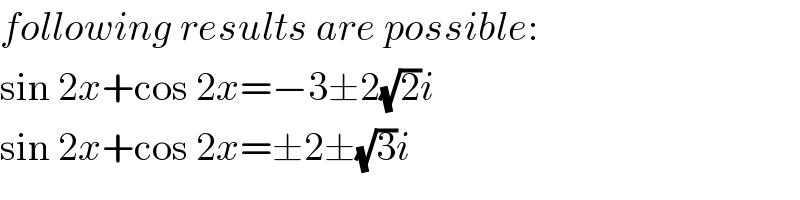
following results are possible: sin 2x+cos 2x=−3±2(√2)i sin 2x+cos 2x=±2±(√3)i

$${following}\:{results}\:{are}\:{possible}: \\ $$$$\mathrm{sin}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{2}{x}=−\mathrm{3}\pm\mathrm{2}\sqrt{\mathrm{2}}{i} \\ $$$$\mathrm{sin}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{2}{x}=\pm\mathrm{2}\pm\sqrt{\mathrm{3}}{i} \\ $$

Commented by MJS last updated on 10/Feb/20

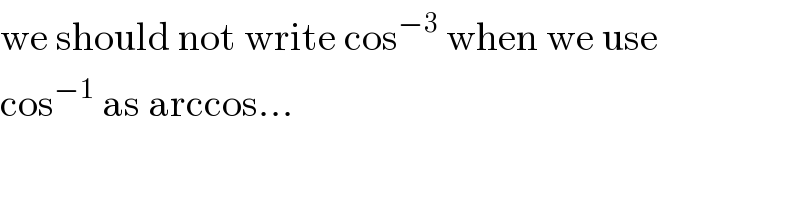
we should not write cos^(−3) when we use cos^(−1) as arccos...

$$\mathrm{we}\:\mathrm{should}\:\mathrm{not}\:\mathrm{write}\:\mathrm{cos}^{−\mathrm{3}} \:\mathrm{when}\:\mathrm{we}\:\mathrm{use} \\ $$$$\mathrm{cos}^{−\mathrm{1}} \:\mathrm{as}\:\mathrm{arccos}… \\ $$

Commented by jagoll last updated on 10/Feb/20

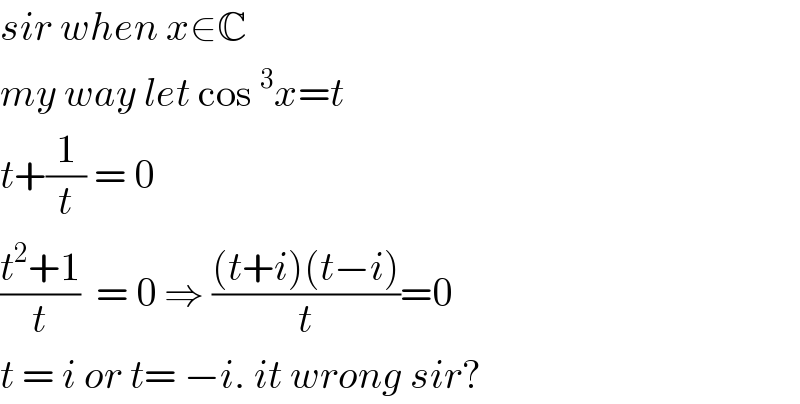
sir when x∈C my way let cos^3 x=t t+(1/t) = 0 ((t^2 +1)/t) = 0 ⇒ (((t+i)(t−i))/t)=0 t = i or t= −i. it wrong sir?

$${sir}\:{when}\:{x}\in\mathbb{C} \\ $$$${my}\:{way}\:{let}\:\mathrm{cos}\:^{\mathrm{3}} {x}={t} \\ $$$${t}+\frac{\mathrm{1}}{{t}}\:=\:\mathrm{0} \\ $$$$\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}}\:\:=\:\mathrm{0}\:\Rightarrow\:\frac{\left({t}+{i}\right)\left({t}−{i}\right)}{{t}}=\mathrm{0} \\ $$$${t}\:=\:{i}\:{or}\:{t}=\:−{i}.\:{it}\:{wrong}\:{sir}? \\ $$

Commented by mr W last updated on 10/Feb/20

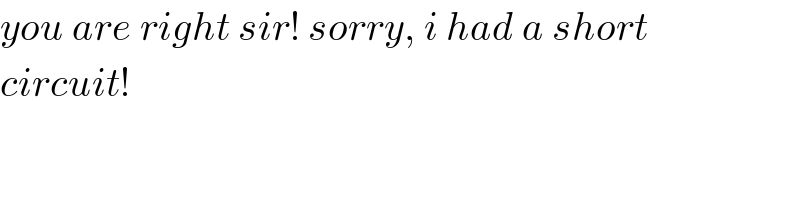
$${you}\:{are}\:{right}\:{sir}!\:{sorry},\:{i}\:{had}\:{a}\:{short} \\ $$$${circuit}! \\ $$

Commented by jagoll last updated on 10/Feb/20

$${yes}\:{sir}.\: \\ $$

Facebook Tweet Pin

if-cos-3-x-cos-3-x-0-find-sin-2x-cos-2x-

Leave a Reply Cancel reply