Question Number 114100 by faysal last updated on 17/Sep/20
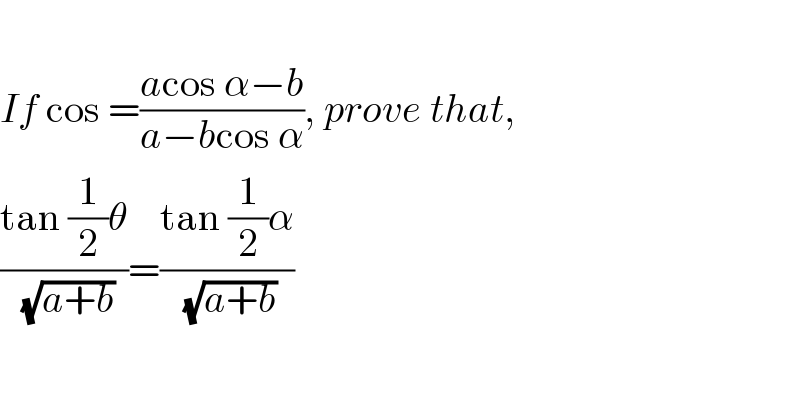
$$ \\ $$$${If}\:\mathrm{cos}\:=\frac{{a}\mathrm{cos}\:\alpha−{b}}{{a}−{b}\mathrm{cos}\:\alpha},\:{prove}\:{that}, \\ $$$$\frac{\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}\theta}{\:\sqrt{{a}+{b}}}=\frac{\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}\alpha}{\:\sqrt{{a}+{b}}} \\ $$
Commented by Henri Boucatchou last updated on 17/Sep/20

$${cos}?=\frac{{acos}\alpha….}{} \\ $$
Commented by som(math1967) last updated on 17/Sep/20
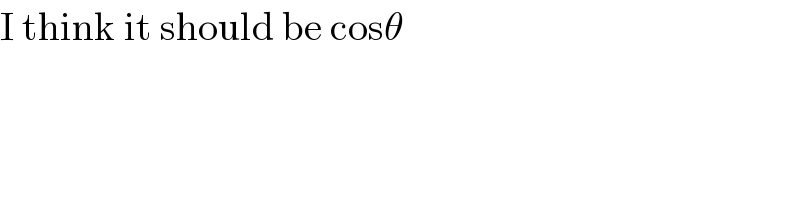
$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{cos}\theta \\ $$
Answered by som(math1967) last updated on 17/Sep/20
![(1/(cosθ))=((a−bcosα)/(acosα−b)) ((1+cosθ)/(1−cosθ))=((a−b+(a−b)cosα)/((a+b)−(a+b)cosα)) [using componendo and dividendo] (1/(tan^2 (θ/2)))=(((a−b)(1+cosα))/((a+b)(1−cosα))) tan^2 (θ/2)=(((a+b))/((a−b)))tan^2 (α/2) tan(θ/2)=(√((a+b)/(a−b)))tan(α/2) ((tan(θ/2))/( (√(a+b))))=((tan(α/2))/( (√(a−b)))) (proved)](https://www.tinkutara.com/question/Q114106.png)
$$\frac{\mathrm{1}}{\mathrm{cos}\theta}=\frac{\mathrm{a}−\mathrm{bcos}\alpha}{\mathrm{acos}\alpha−\mathrm{b}} \\ $$$$\frac{\mathrm{1}+\mathrm{cos}\theta}{\mathrm{1}−\mathrm{cos}\theta}=\frac{\mathrm{a}−\mathrm{b}+\left(\mathrm{a}−\mathrm{b}\right)\mathrm{cos}\alpha}{\left(\mathrm{a}+\mathrm{b}\right)−\left(\mathrm{a}+\mathrm{b}\right)\mathrm{cos}\alpha} \\ $$$$\left[\mathrm{using}\:\mathrm{componendo}\:\mathrm{and}\:\mathrm{dividendo}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}=\frac{\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{1}+\mathrm{cos}\alpha\right)}{\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{1}−\mathrm{cos}\alpha\right)} \\ $$$$\mathrm{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}=\frac{\left(\mathrm{a}+\mathrm{b}\right)}{\left(\mathrm{a}−\mathrm{b}\right)}\mathrm{tan}^{\mathrm{2}} \frac{\alpha}{\mathrm{2}} \\ $$$$\mathrm{tan}\frac{\theta}{\mathrm{2}}=\sqrt{\frac{\mathrm{a}+\mathrm{b}}{\mathrm{a}−\mathrm{b}}}\mathrm{tan}\frac{\alpha}{\mathrm{2}} \\ $$$$\frac{\mathrm{tan}\frac{\theta}{\mathrm{2}}}{\:\sqrt{\mathrm{a}+\mathrm{b}}}=\frac{\mathrm{tan}\frac{\alpha}{\mathrm{2}}}{\:\sqrt{\mathrm{a}−\mathrm{b}}}\:\left(\mathrm{proved}\right) \\ $$
