Question Number 79086 by key of knowledge last updated on 22/Jan/20
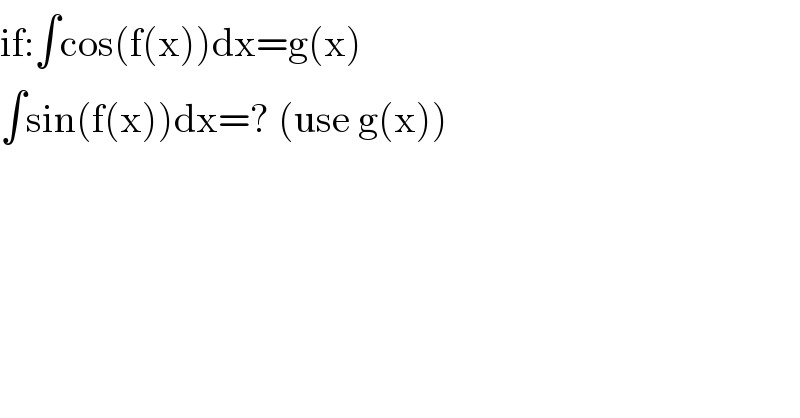
$$\mathrm{if}:\int\mathrm{cos}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\mathrm{dx}=\mathrm{g}\left(\mathrm{x}\right) \\ $$$$\int\mathrm{sin}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\mathrm{dx}=?\:\left(\mathrm{use}\:\mathrm{g}\left(\mathrm{x}\right)\right) \\ $$
Commented by mr W last updated on 23/Jan/20
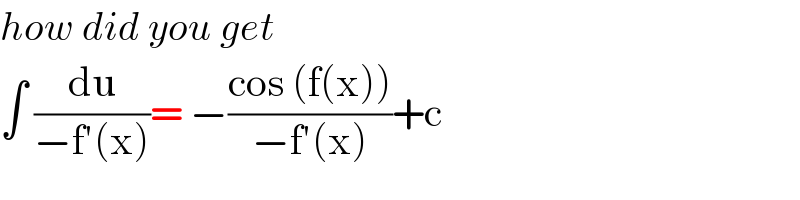
$${how}\:{did}\:{you}\:{get} \\ $$$$\int\:\frac{\mathrm{du}}{−\mathrm{f}'\left(\mathrm{x}\right)}=\:−\frac{\mathrm{cos}\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)}{−\mathrm{f}'\left(\mathrm{x}\right)}+\mathrm{c} \\ $$
Commented by jagoll last updated on 23/Jan/20
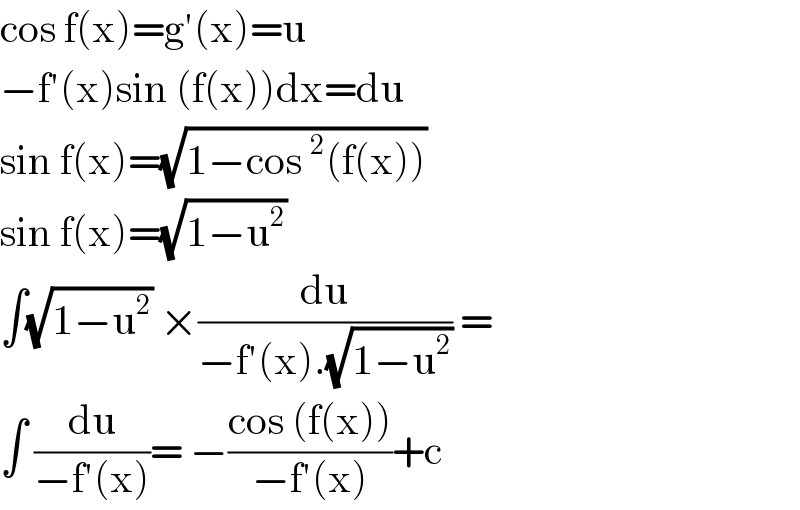
$$\mathrm{cos}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{g}'\left(\mathrm{x}\right)=\mathrm{u} \\ $$$$−\mathrm{f}'\left(\mathrm{x}\right)\mathrm{sin}\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)\mathrm{dx}=\mathrm{du} \\ $$$$\mathrm{sin}\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)} \\ $$$$\mathrm{sin}\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} } \\ $$$$\int\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\:×\frac{\mathrm{du}}{−\mathrm{f}'\left(\mathrm{x}\right).\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}\:= \\ $$$$\int\:\frac{\mathrm{du}}{−\mathrm{f}'\left(\mathrm{x}\right)}=\:−\frac{\mathrm{cos}\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)}{−\mathrm{f}'\left(\mathrm{x}\right)}+\mathrm{c} \\ $$
