Question Number 175879 by cortano1 last updated on 08/Sep/22
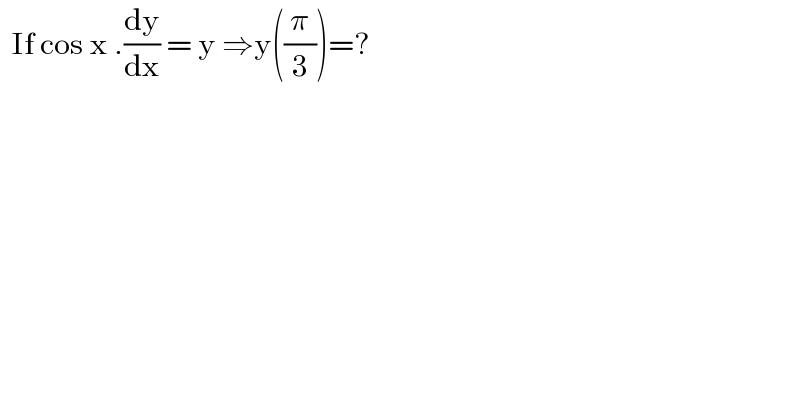
$$\:\:\mathrm{If}\:\mathrm{cos}\:\mathrm{x}\:.\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{y}\:\Rightarrow\mathrm{y}\left(\frac{\pi}{\mathrm{3}}\right)=? \\ $$
Commented by mr W last updated on 08/Sep/22
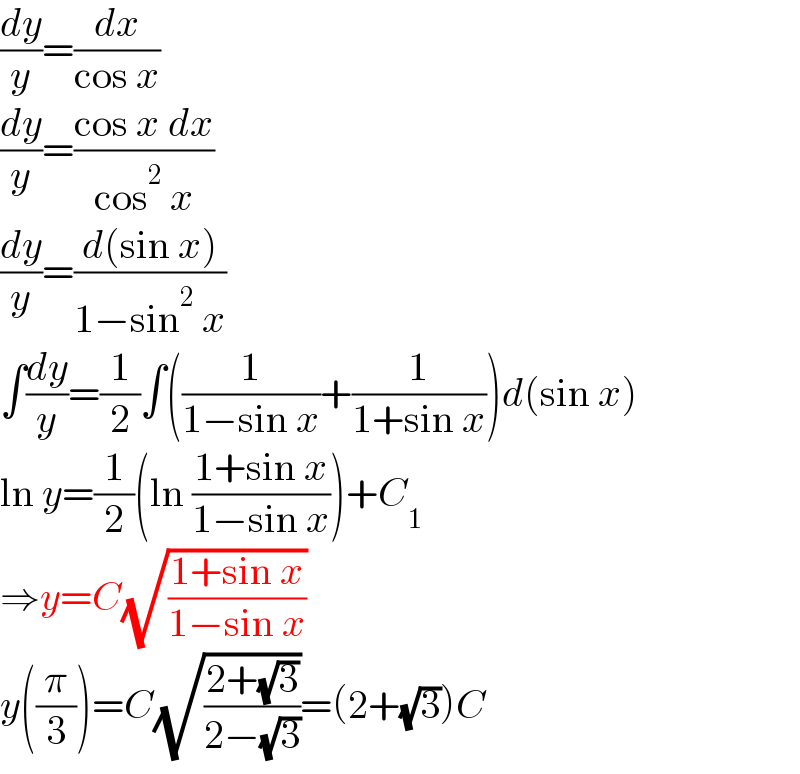
$$\frac{{dy}}{{y}}=\frac{{dx}}{\mathrm{cos}\:{x}} \\ $$$$\frac{{dy}}{{y}}=\frac{\mathrm{cos}\:{x}\:{dx}}{\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$\frac{{dy}}{{y}}=\frac{{d}\left(\mathrm{sin}\:{x}\right)}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}} \\ $$$$\int\frac{{dy}}{{y}}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{x}}\right){d}\left(\mathrm{sin}\:{x}\right) \\ $$$$\mathrm{ln}\:{y}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\:\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}\right)+{C}_{\mathrm{1}} \\ $$$$\Rightarrow{y}={C}\sqrt{\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}} \\ $$$${y}\left(\frac{\pi}{\mathrm{3}}\right)={C}\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}−\sqrt{\mathrm{3}}}}=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){C} \\ $$
Commented by cortano1 last updated on 09/Sep/22

$$\mathrm{yes}…\mathrm{I}\:\mathrm{got}\: \\ $$$$\:\mathrm{y}\:=\:\frac{\mathrm{C}\:\mathrm{cos}\:\mathrm{x}}{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}\: \\ $$
