Question Number 34980 by NECx last updated on 14/May/18
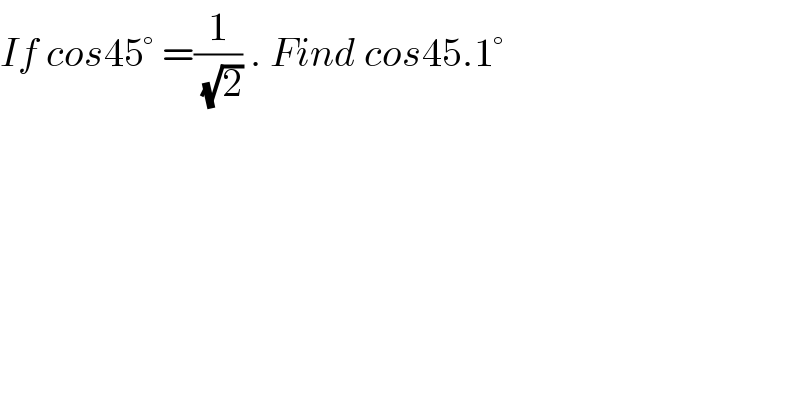
$${If}\:{cos}\mathrm{45}°\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:.\:{Find}\:{cos}\mathrm{45}.\mathrm{1}° \\ $$
Answered by ajfour last updated on 14/May/18
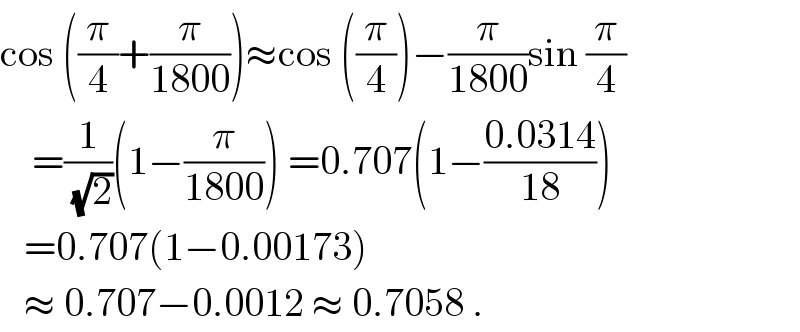
$$\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{1800}}\right)\approx\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}\right)−\frac{\pi}{\mathrm{1800}}\mathrm{sin}\:\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}−\frac{\pi}{\mathrm{1800}}\right)\:=\mathrm{0}.\mathrm{707}\left(\mathrm{1}−\frac{\mathrm{0}.\mathrm{0314}}{\mathrm{18}}\right) \\ $$$$\:\:\:=\mathrm{0}.\mathrm{707}\left(\mathrm{1}−\mathrm{0}.\mathrm{00173}\right) \\ $$$$\:\:\:\approx\:\mathrm{0}.\mathrm{707}−\mathrm{0}.\mathrm{0012}\:\approx\:\mathrm{0}.\mathrm{7058}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/May/18
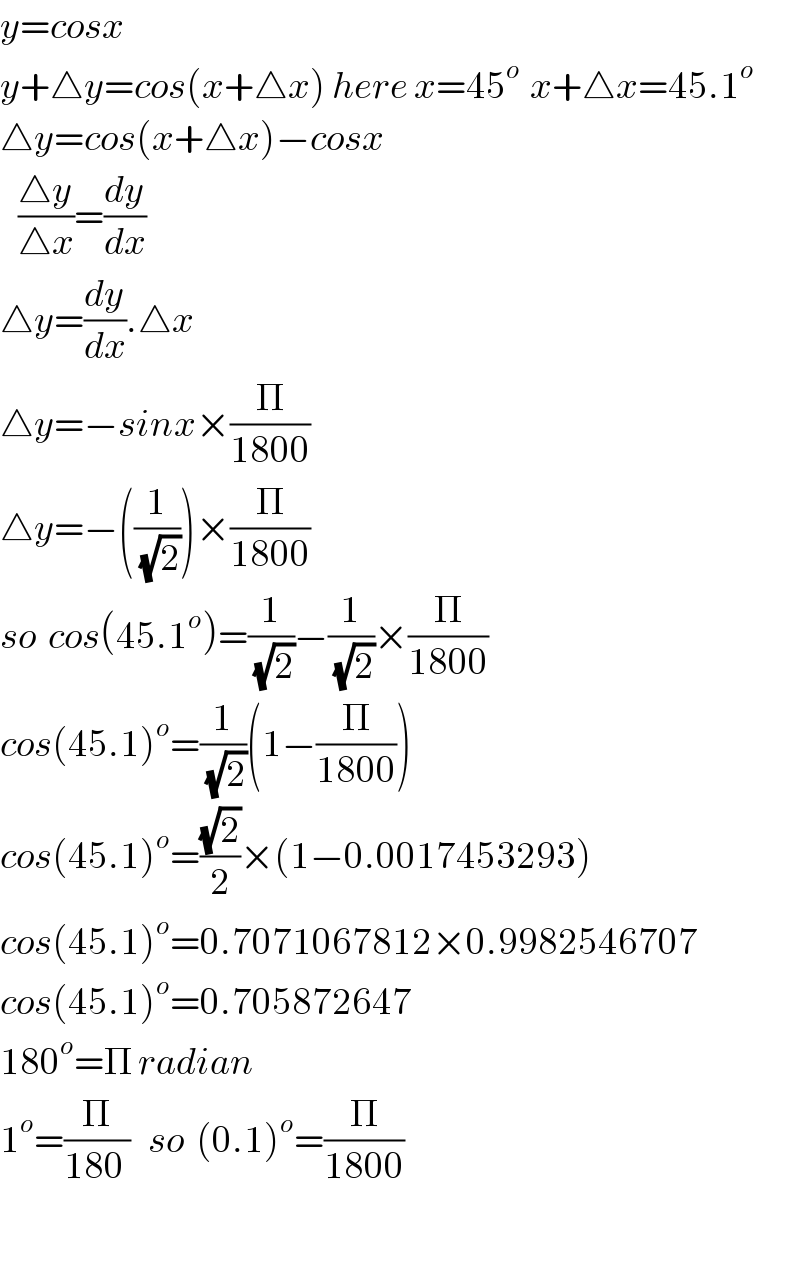
$${y}={cosx} \\ $$$${y}+\bigtriangleup{y}={cos}\left({x}+\bigtriangleup{x}\right)\:{here}\:{x}=\mathrm{45}^{{o}\:} \:{x}+\bigtriangleup{x}=\mathrm{45}.\mathrm{1}^{{o}} \\ $$$$\bigtriangleup{y}={cos}\left({x}+\bigtriangleup{x}\right)−{cosx} \\ $$$$\:\:\:\frac{\bigtriangleup{y}}{\bigtriangleup{x}}=\frac{{dy}}{{dx}} \\ $$$$\bigtriangleup{y}=\frac{{dy}}{{dx}}.\bigtriangleup{x} \\ $$$$\bigtriangleup{y}=−{sinx}×\frac{\Pi}{\mathrm{1800}} \\ $$$$\bigtriangleup{y}=−\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)×\frac{\Pi}{\mathrm{1800}} \\ $$$${so}\:\:{cos}\left(\mathrm{45}.\mathrm{1}^{{o}} \right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\frac{\Pi}{\mathrm{1800}} \\ $$$${cos}\left(\mathrm{45}.\mathrm{1}\right)^{{o}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}−\frac{\Pi}{\mathrm{1800}}\right) \\ $$$${cos}\left(\mathrm{45}.\mathrm{1}\right)^{{o}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×\left(\mathrm{1}−\mathrm{0}.\mathrm{0017453293}\right) \\ $$$${cos}\left(\mathrm{45}.\mathrm{1}\right)^{{o}} =\mathrm{0}.\mathrm{7071067812}×\mathrm{0}.\mathrm{9982546707} \\ $$$${cos}\left(\mathrm{45}.\mathrm{1}\right)^{{o}} =\mathrm{0}.\mathrm{705872647} \\ $$$$\mathrm{180}^{{o}} =\Pi\:{radian} \\ $$$$\mathrm{1}^{{o}} =\frac{\Pi}{\mathrm{180}\:}\:\:\:{so}\:\:\left(\mathrm{0}.\mathrm{1}\right)^{{o}} =\frac{\Pi}{\mathrm{1800}} \\ $$$$ \\ $$
