Question Number 61823 by necx1 last updated on 09/Jun/19
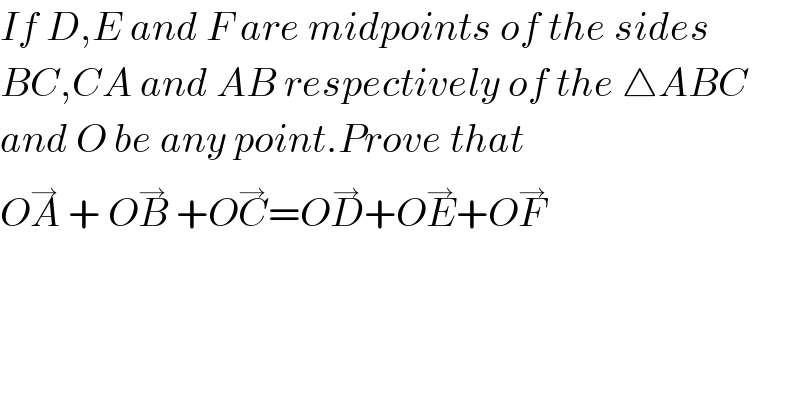
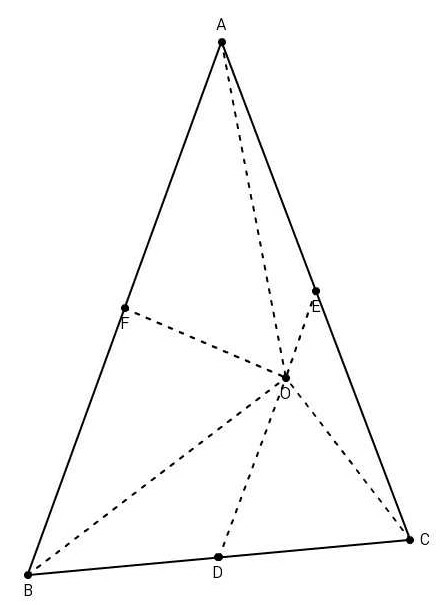
$${If}\:{D},{E}\:{and}\:{F}\:{are}\:{midpoints}\:{of}\:{the}\:{sides} \\ $$$${BC},{CA}\:{and}\:{AB}\:{respectively}\:{of}\:{the}\:\bigtriangleup{ABC} \\ $$$${and}\:{O}\:{be}\:{any}\:{point}.{Prove}\:{that} \\ $$$${O}\overset{\rightarrow} {{A}}\:+\:{O}\overset{\rightarrow} {{B}}\:+{O}\overset{\rightarrow} {{C}}={O}\overset{\rightarrow} {{D}}+{O}\overset{\rightarrow} {{E}}+{O}\overset{\rightarrow} {{F}} \\ $$
Answered by Kunal12588 last updated on 09/Jun/19
![In △AOF OA^(→) +AF^(→) +FO^(→) =0 (1) In △BOF OB^(→) +BF^(→) +FO^(→) =0 (2) adding (1) and (2) OA^(→) +OB^(→) +(AF^(→) +BF^(→) )+2∙FO^(→) =0 ⇒2∙OF^(→) =OA^(→) +OB^(→) [∵AF^(→) +BF^(→) =0, OF^(→) =−FO^(→) ] similarly 2∙OD^(→) =OB^(→) +OC^(→) 2∙OE^(→) =OA^(→) +OC^(→) adding blue ones 2(OD^(→) +OE^(→) +OF^(→) )=2(OA^(→) +OB^(→) +OC^(→) ) ⇒ OD^(→) +OE^(→) +OF^(→) =OA^(→) +OB^(→) +OC^(→) proved](https://www.tinkutara.com/question/Q61828.png)
$$\mathrm{In}\:\bigtriangleup\mathrm{AOF} \\ $$$$\overset{\rightarrow} {\mathrm{OA}}+\overset{\rightarrow} {\mathrm{AF}}+\overset{\rightarrow} {\mathrm{FO}}=\mathrm{0}\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{In}\:\bigtriangleup\mathrm{BOF} \\ $$$$\overset{\rightarrow} {\mathrm{OB}}+\overset{\rightarrow} {\mathrm{BF}}+\overset{\rightarrow} {\mathrm{FO}}=\mathrm{0}\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\mathrm{adding}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right) \\ $$$$\overset{\rightarrow} {\mathrm{OA}}+\overset{\rightarrow} {\mathrm{OB}}+\left(\overset{\rightarrow} {\mathrm{AF}}+\overset{\rightarrow} {\mathrm{BF}}\right)+\mathrm{2}\centerdot\overset{\rightarrow} {\mathrm{FO}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\centerdot\overset{\rightarrow} {\mathrm{OF}}=\overset{\rightarrow} {\mathrm{OA}}+\overset{\rightarrow} {\mathrm{OB}}\:\:\:\left[\because\overset{\rightarrow} {\mathrm{AF}}+\overset{\rightarrow} {\mathrm{BF}}=\mathrm{0},\:\overset{\rightarrow} {\mathrm{OF}}=−\overset{\rightarrow} {\mathrm{FO}}\right] \\ $$$$\mathrm{similarly} \\ $$$$\mathrm{2}\centerdot\overset{\rightarrow} {\mathrm{OD}}=\overset{\rightarrow} {\mathrm{OB}}+\overset{\rightarrow} {\mathrm{OC}} \\ $$$$\mathrm{2}\centerdot\overset{\rightarrow} {\mathrm{OE}}=\overset{\rightarrow} {\mathrm{OA}}+\overset{\rightarrow} {\mathrm{OC}} \\ $$$$\mathrm{adding}\:\mathrm{blue}\:\mathrm{ones} \\ $$$$\mathrm{2}\left(\overset{\rightarrow} {\mathrm{OD}}+\overset{\rightarrow} {\mathrm{OE}}+\overset{\rightarrow} {\mathrm{OF}}\right)=\mathrm{2}\left(\overset{\rightarrow} {\mathrm{OA}}+\overset{\rightarrow} {\mathrm{OB}}+\overset{\rightarrow} {\mathrm{OC}}\right) \\ $$$$\Rightarrow\:\overset{\rightarrow} {\mathrm{OD}}+\overset{\rightarrow} {\mathrm{OE}}+\overset{\rightarrow} {\mathrm{OF}}=\overset{\rightarrow} {\mathrm{OA}}+\overset{\rightarrow} {\mathrm{OB}}+\overset{\rightarrow} {\mathrm{OC}}\:\:\mathrm{proved} \\ $$
Commented by Kunal12588 last updated on 09/Jun/19