Question Number 87419 by john santu last updated on 04/Apr/20
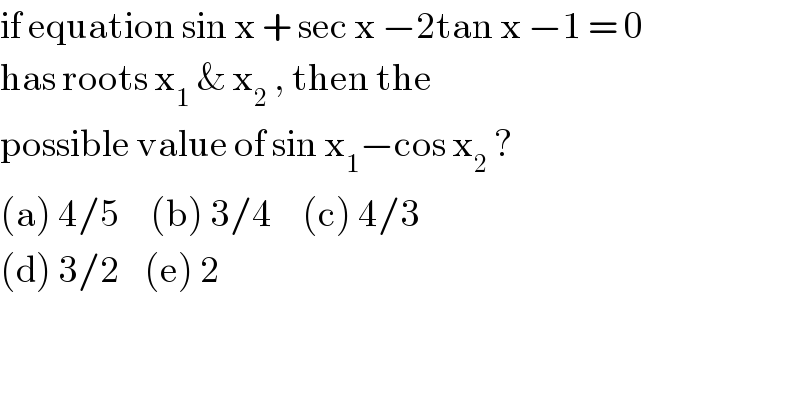
Commented by john santu last updated on 04/Apr/20
Commented by MJS last updated on 04/Apr/20
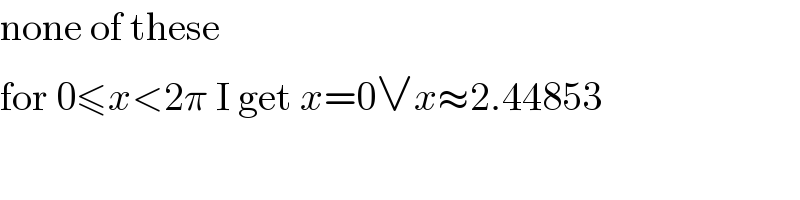
Commented by john santu last updated on 04/Apr/20
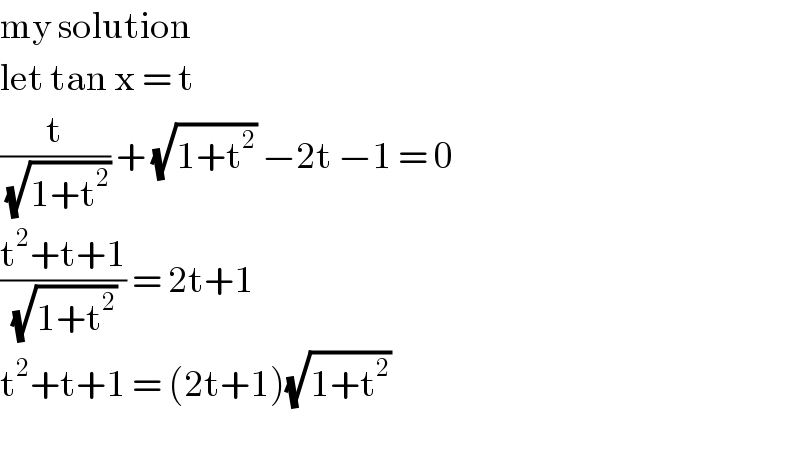
Commented by john santu last updated on 04/Apr/20

Commented by MJS last updated on 04/Apr/20

Commented by john santu last updated on 04/Apr/20

Answered by MJS last updated on 04/Apr/20

Commented by john santu last updated on 04/Apr/20

Commented by MJS last updated on 04/Apr/20
![x^3 +ax^2 +bx+c=0 let x=t−(a/3) t^3 −((a^2 −3b)/3)t+((2a^3 −9ab+27c)/(27))=0 −((a^2 −3b)/3)=p∧((2a^3 −9ab+27c)/(27))=q t^3 +pt+q=0 D=(p^3 /(27))+(q^2 /4) { ((>0 ⇒ Cardano)),((<0 ⇒ trigonimetric solution)) :} Cardano u=((−(q/2)+(√((p^3 /(27))+(q^2 /4)))))^(1/3) v=((−(q/2)−(√((p^3 /(27))+(q^2 /4)))))^(1/3) [we need the real roots i.e. ((−1))^(1/3) =−1] t_1 =u+v t_2 =(−(1/2)−((√3)/2)i)u+(−(1/2)+((√3)/2)i)v t_3 =(−(1/2)+((√3)/2)i)u+(−(1/2)−((√3)/2)i)v trigononetric solution t_(j+1) =((2(√(−3p)))/3)sin (((2jπ)/3)−(1/3)arcsin ((3(√3)q)/(2p(√(−p))))) with j=0, 1, 2](https://www.tinkutara.com/question/Q87450.png)
