Question Number 83871 by jagoll last updated on 07/Mar/20
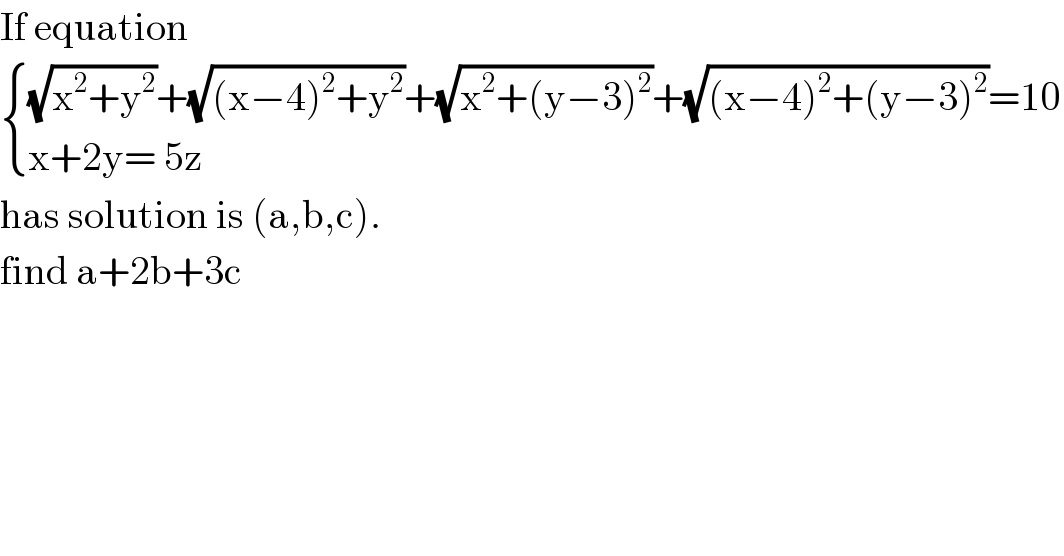
$$\mathrm{If}\:\mathrm{equation}\: \\ $$$$\begin{cases}{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }+\sqrt{\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }+\sqrt{\mathrm{x}^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} }=\mathrm{10}}\\{\mathrm{x}+\mathrm{2y}=\:\mathrm{5z}}\end{cases} \\ $$$$\mathrm{has}\:\mathrm{solution}\:\mathrm{is}\:\left(\mathrm{a},\mathrm{b},\mathrm{c}\right).\: \\ $$$$\mathrm{find}\:\mathrm{a}+\mathrm{2b}+\mathrm{3c}\: \\ $$
Commented by mr W last updated on 07/Mar/20

$${way}\:\mathrm{1}: \\ $$$${let}\:{f}\left({x},{y}\right)=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }+\sqrt{\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }+\sqrt{\mathrm{x}^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${with}\:\frac{\partial{f}}{\partial{x}}=\mathrm{0},\:\frac{\partial{f}}{\partial{y}}=\mathrm{0} \\ $$$${you}\:{can}\:{get}\:{f}\left({x},{y}\right)_{{min}} =\mathrm{10}\:{at}\:{x}=\mathrm{2},\:{y}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({x},{y}\right)=\mathrm{10}\:{has}\:{only}\:{one}\:{solution}: \\ $$$${x}=\mathrm{2}\:{and}\:{y}=\frac{\mathrm{3}}{\mathrm{2}}. \\ $$$$ \\ $$$${way}\:\mathrm{2}: \\ $$$${LHS}=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }+\sqrt{\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }+\sqrt{\mathrm{x}^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${is}\:{the}\:{sum}\:{of}\:{distances}\:{from}\:{a}\:{point} \\ $$$$\left({x},{y}\right)\:{to}\:{the}\:\mathrm{4}\:{vertices}\:{of}\:{a}\:{rectangle} \\ $$$${with}\:{side}\:{lengthes}\:\mathrm{4}\:{and}\:\mathrm{3}. \\ $$$${the}\:{smallest}\:{sum}\:{is}\:{when}\:{this}\:{point} \\ $$$${is}\:{at}\:{the}\:{center}\:{of}\:{the}\:{rectangle}\:{which} \\ $$$${lies}\:{at}\:\left(\mathrm{2},\frac{\mathrm{3}}{\mathrm{2}}\right).\:{the}\:{smallest}\:{sum}\:{is}\:{the} \\ $$$${lengthes}\:{of}\:{both}\:{diagonals},\:{i}.{e}.\:\mathrm{2}×\mathrm{5}=\mathrm{10}. \\ $$$${that}\:{means}\:{LHS}\geqslant\mathrm{10}.\:{for}\:{LHS}=\mathrm{10} \\ $$$${there}\:{is}\:{only}\:{one}\:{solution}: \\ $$$${x}=\mathrm{2},\:{y}=\frac{\mathrm{3}}{\mathrm{2}}. \\ $$
Commented by mr W last updated on 07/Mar/20
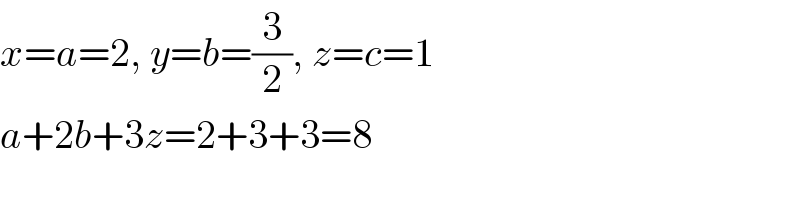
$${x}={a}=\mathrm{2},\:{y}={b}=\frac{\mathrm{3}}{\mathrm{2}},\:{z}={c}=\mathrm{1} \\ $$$${a}+\mathrm{2}{b}+\mathrm{3}{z}=\mathrm{2}+\mathrm{3}+\mathrm{3}=\mathrm{8} \\ $$
Commented by jagoll last updated on 07/Mar/20

$$\mathrm{how}\:\mathrm{to}\:\mathrm{got}\:\mathrm{it}\:\mathrm{sir}? \\ $$
Commented by jagoll last updated on 07/Mar/20
$$\mathrm{why}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{blank}\:\mathrm{sir} \\ $$
