Question Number 154359 by ZiYangLee last updated on 17/Sep/21
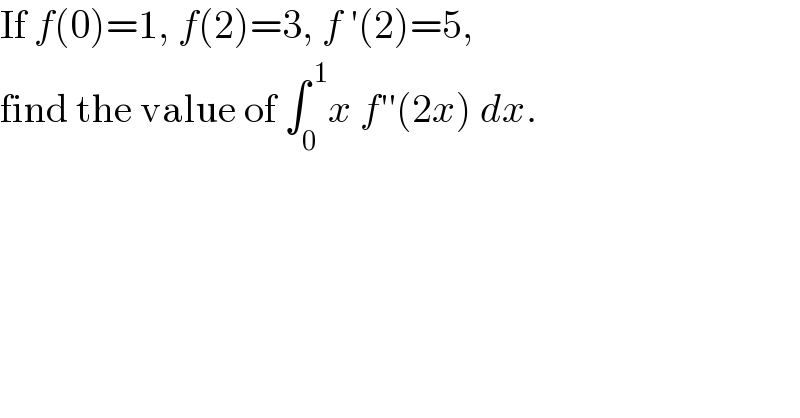
$$\mathrm{If}\:{f}\left(\mathrm{0}\right)=\mathrm{1},\:{f}\left(\mathrm{2}\right)=\mathrm{3},\:{f}\:'\left(\mathrm{2}\right)=\mathrm{5}, \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}\:{f}''\left(\mathrm{2}{x}\right)\:{dx}. \\ $$
Answered by aleks041103 last updated on 17/Sep/21
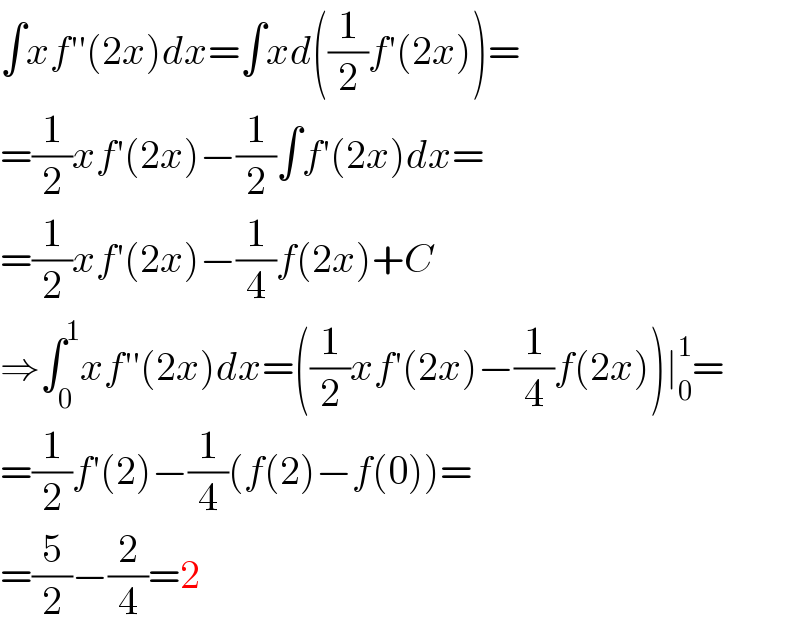
$$\int{xf}''\left(\mathrm{2}{x}\right){dx}=\int{xd}\left(\frac{\mathrm{1}}{\mathrm{2}}{f}'\left(\mathrm{2}{x}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{xf}'\left(\mathrm{2}{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int{f}'\left(\mathrm{2}{x}\right){dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{xf}'\left(\mathrm{2}{x}\right)−\frac{\mathrm{1}}{\mathrm{4}}{f}\left(\mathrm{2}{x}\right)+{C} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {xf}''\left(\mathrm{2}{x}\right){dx}=\left(\frac{\mathrm{1}}{\mathrm{2}}{xf}'\left(\mathrm{2}{x}\right)−\frac{\mathrm{1}}{\mathrm{4}}{f}\left(\mathrm{2}{x}\right)\right)\mid_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{f}'\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{4}}\left({f}\left(\mathrm{2}\right)−{f}\left(\mathrm{0}\right)\right)= \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}−\frac{\mathrm{2}}{\mathrm{4}}=\mathrm{2} \\ $$
