Question Number 144629 by mathdanisur last updated on 27/Jun/21
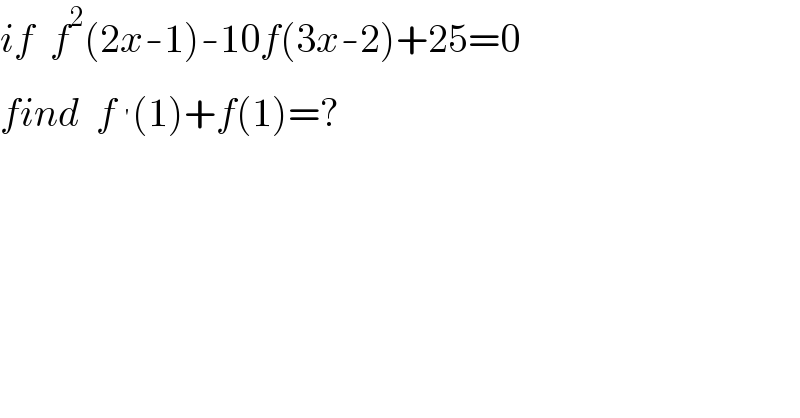
$${if}\:\:{f}^{\mathrm{2}} \left(\mathrm{2}{x}-\mathrm{1}\right)-\mathrm{10}{f}\left(\mathrm{3}{x}-\mathrm{2}\right)+\mathrm{25}=\mathrm{0} \\ $$$${find}\:\:{f}\:^{'} \left(\mathrm{1}\right)+{f}\left(\mathrm{1}\right)=? \\ $$
Answered by liberty last updated on 27/Jun/21
![[f(2x−1)]^2 −10f(3x−2)+25=0 (d/dx)[ (f(2x−1))^2 −10f(3x−2)+25]=0 ⇒2.2 f(2x−1)f ′(2x−1)−30f ′(3x−2)=0 case(1)2x−1=1 ; x=1 →4f(1).f ′(1)−30f ′(1)=0 ⇒f ′(1) {4f(1)−30}=0 { ((f ′(1)=0)),((f(1)=((15)/2) (rejected))) :} case(2) inserting x=1 to original equation ⇒[f(1)]^2 −10f(1)+25 = 0 ⇒(f(1)−5)^2 =0 ⇒f(1)=5 therefore f ′(1)+f(1)= 0+5 = 5](https://www.tinkutara.com/question/Q144635.png)
$$\left[\mathrm{f}\left(\mathrm{2x}−\mathrm{1}\right)\right]^{\mathrm{2}} −\mathrm{10f}\left(\mathrm{3x}−\mathrm{2}\right)+\mathrm{25}=\mathrm{0} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left[\:\left(\mathrm{f}\left(\mathrm{2x}−\mathrm{1}\right)\right)^{\mathrm{2}} −\mathrm{10f}\left(\mathrm{3x}−\mathrm{2}\right)+\mathrm{25}\right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}.\mathrm{2}\:\mathrm{f}\left(\mathrm{2x}−\mathrm{1}\right)\mathrm{f}\:'\left(\mathrm{2x}−\mathrm{1}\right)−\mathrm{30f}\:'\left(\mathrm{3x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\mathrm{2x}−\mathrm{1}=\mathrm{1}\:;\:\mathrm{x}=\mathrm{1} \\ $$$$\rightarrow\mathrm{4f}\left(\mathrm{1}\right).\mathrm{f}\:'\left(\mathrm{1}\right)−\mathrm{30f}\:'\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{f}\:'\left(\mathrm{1}\right)\:\left\{\mathrm{4f}\left(\mathrm{1}\right)−\mathrm{30}\right\}=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{f}\:'\left(\mathrm{1}\right)=\mathrm{0}}\\{\mathrm{f}\left(\mathrm{1}\right)=\frac{\mathrm{15}}{\mathrm{2}}\:\left(\mathrm{rejected}\right)}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{inserting}\:\mathrm{x}=\mathrm{1}\:\mathrm{to}\:\mathrm{original} \\ $$$$\mathrm{equation} \\ $$$$\Rightarrow\left[\mathrm{f}\left(\mathrm{1}\right)\right]^{\mathrm{2}} −\mathrm{10f}\left(\mathrm{1}\right)+\mathrm{25}\:=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{f}\left(\mathrm{1}\right)−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\mathrm{f}\left(\mathrm{1}\right)=\mathrm{5}\: \\ $$$$\mathrm{therefore}\:\mathrm{f}\:'\left(\mathrm{1}\right)+\mathrm{f}\left(\mathrm{1}\right)=\:\mathrm{0}+\mathrm{5}\:=\:\mathrm{5} \\ $$
Commented by mathdanisur last updated on 27/Jun/21
$${alot}\:{cool}\:{thank}\:{you}\:{Sir} \\ $$
