Question Number 124444 by benjo_mathlover last updated on 03/Dec/20
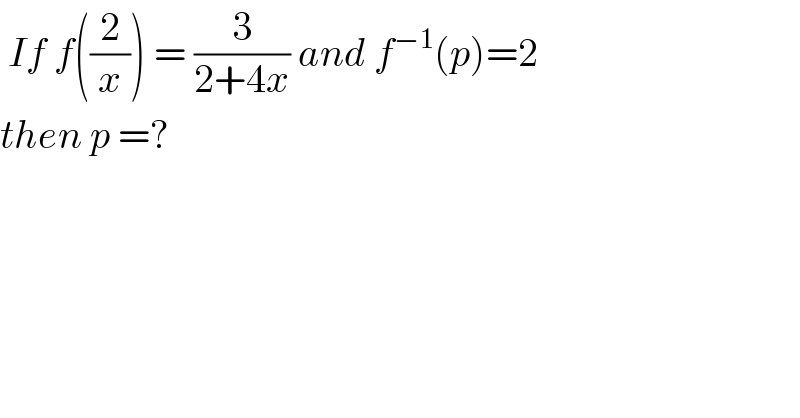
$$\:{If}\:{f}\left(\frac{\mathrm{2}}{{x}}\right)\:=\:\frac{\mathrm{3}}{\mathrm{2}+\mathrm{4}{x}}\:{and}\:{f}^{−\mathrm{1}} \left({p}\right)=\mathrm{2}\: \\ $$$${then}\:{p}\:=? \\ $$
Answered by bemath last updated on 03/Dec/20
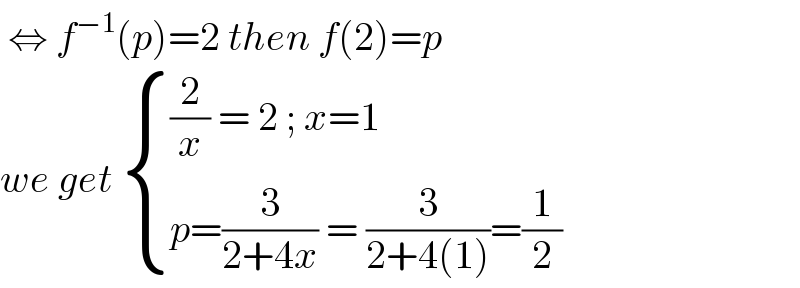
$$\:\Leftrightarrow\:{f}^{−\mathrm{1}} \left({p}\right)=\mathrm{2}\:{then}\:{f}\left(\mathrm{2}\right)={p} \\ $$$${we}\:{get}\:\begin{cases}{\frac{\mathrm{2}}{{x}}\:=\:\mathrm{2}\:;\:{x}=\mathrm{1}}\\{{p}=\frac{\mathrm{3}}{\mathrm{2}+\mathrm{4}{x}}\:=\:\frac{\mathrm{3}}{\mathrm{2}+\mathrm{4}\left(\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$
Answered by mathmax by abdo last updated on 03/Dec/20
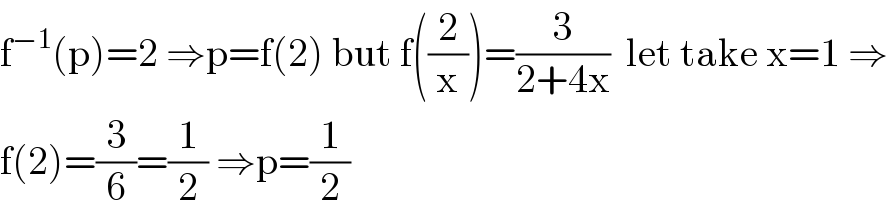
$$\mathrm{f}^{−\mathrm{1}} \left(\mathrm{p}\right)=\mathrm{2}\:\Rightarrow\mathrm{p}=\mathrm{f}\left(\mathrm{2}\right)\:\mathrm{but}\:\mathrm{f}\left(\frac{\mathrm{2}}{\mathrm{x}}\right)=\frac{\mathrm{3}}{\mathrm{2}+\mathrm{4x}}\:\:\mathrm{let}\:\mathrm{take}\:\mathrm{x}=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{2}\right)=\frac{\mathrm{3}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{p}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
