Question Number 150652 by mathdanisur last updated on 14/Aug/21
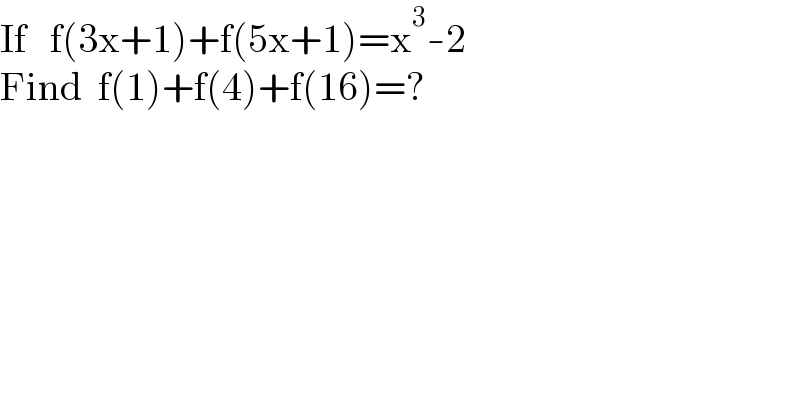
$$\mathrm{If}\:\:\:\mathrm{f}\left(\mathrm{3x}+\mathrm{1}\right)+\mathrm{f}\left(\mathrm{5x}+\mathrm{1}\right)=\mathrm{x}^{\mathrm{3}} -\mathrm{2} \\ $$$$\mathrm{Find}\:\:\mathrm{f}\left(\mathrm{1}\right)+\mathrm{f}\left(\mathrm{4}\right)+\mathrm{f}\left(\mathrm{16}\right)=? \\ $$
Commented by MJS_new last updated on 14/Aug/21
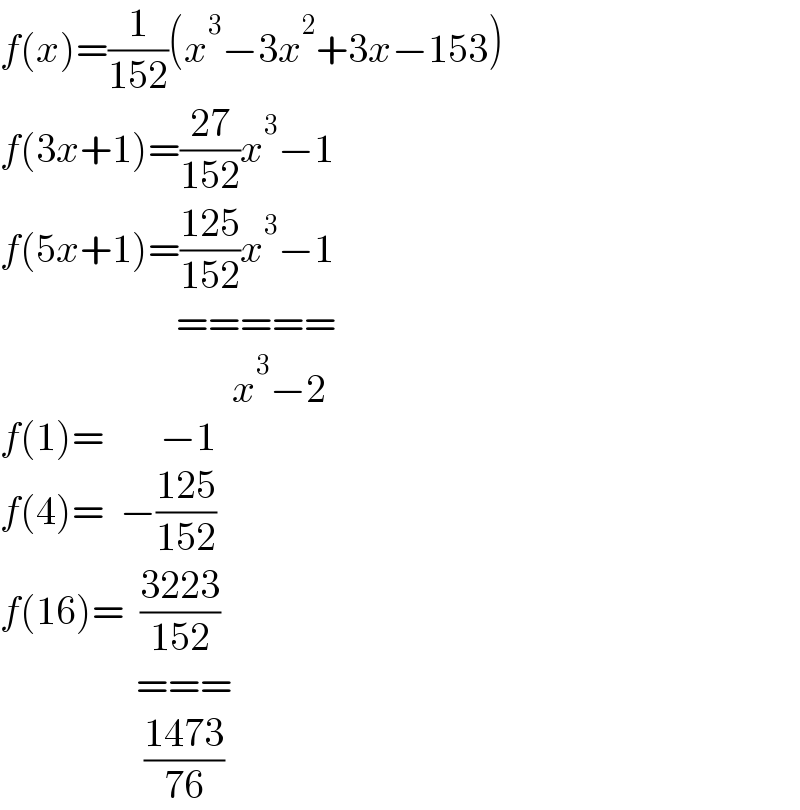
$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{152}}\left({x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{153}\right) \\ $$$${f}\left(\mathrm{3}{x}+\mathrm{1}\right)=\frac{\mathrm{27}}{\mathrm{152}}{x}^{\mathrm{3}} −\mathrm{1} \\ $$$${f}\left(\mathrm{5}{x}+\mathrm{1}\right)=\frac{\mathrm{125}}{\mathrm{152}}{x}^{\mathrm{3}} −\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:===== \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{3}} −\mathrm{2} \\ $$$${f}\left(\mathrm{1}\right)=\:\:\:\:\:\:\:−\mathrm{1} \\ $$$${f}\left(\mathrm{4}\right)=\:\:−\frac{\mathrm{125}}{\mathrm{152}} \\ $$$${f}\left(\mathrm{16}\right)=\:\:\frac{\mathrm{3223}}{\mathrm{152}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=== \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1473}}{\mathrm{76}} \\ $$
Commented by amin96 last updated on 14/Aug/21

$${nice}\:{solution} \\ $$
Commented by JDamian last updated on 14/Aug/21
How do you get the first line?
Commented by MJS_new last updated on 14/Aug/21
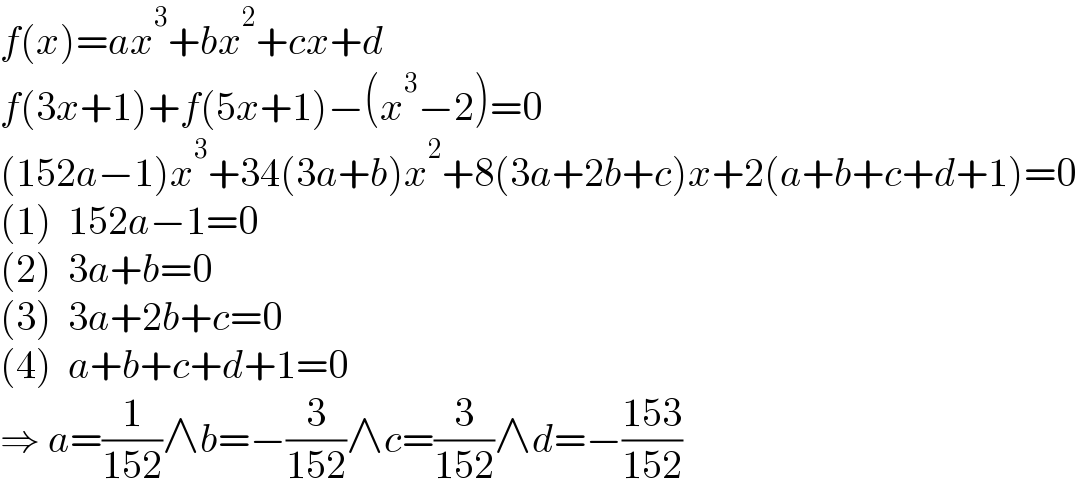
$${f}\left({x}\right)={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${f}\left(\mathrm{3}{x}+\mathrm{1}\right)+{f}\left(\mathrm{5}{x}+\mathrm{1}\right)−\left({x}^{\mathrm{3}} −\mathrm{2}\right)=\mathrm{0} \\ $$$$\left(\mathrm{152}{a}−\mathrm{1}\right){x}^{\mathrm{3}} +\mathrm{34}\left(\mathrm{3}{a}+{b}\right){x}^{\mathrm{2}} +\mathrm{8}\left(\mathrm{3}{a}+\mathrm{2}{b}+{c}\right){x}+\mathrm{2}\left({a}+{b}+{c}+{d}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{152}{a}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:\mathrm{3}{a}+{b}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:\mathrm{3}{a}+\mathrm{2}{b}+{c}=\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\:{a}+{b}+{c}+{d}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{a}=\frac{\mathrm{1}}{\mathrm{152}}\wedge{b}=−\frac{\mathrm{3}}{\mathrm{152}}\wedge{c}=\frac{\mathrm{3}}{\mathrm{152}}\wedge{d}=−\frac{\mathrm{153}}{\mathrm{152}} \\ $$
Commented by mathdanisur last updated on 14/Aug/21
$$\mathrm{Cool}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you} \\ $$
