if-f-f-f-f-x-16x-15-find-f-x-

Question Number 151080 by malwan last updated on 18/Aug/21

i f (f \circ f \circ f \circ f) (x) = 16 x + 15

f i n d f (x)

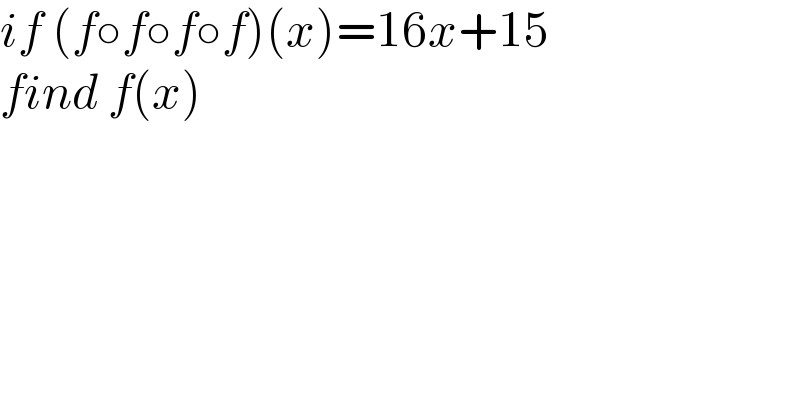
Answered by Mokmokhi last updated on 18/Aug/21

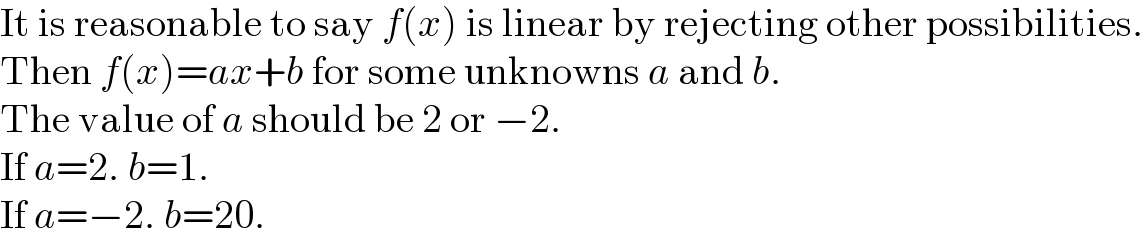
It is reasonable to say f (x) is linear by rejecting other possibilities .

Then f (x) = a x + b for some unknowns a and b .

The value of a should be 2 or - 2 .

If a = 2 . b = 1 .

If a = - 2 . b = 20 .

Commented by malwan last updated on 18/Aug/21

t h a n k y o u s i r

Answered by qaz last updated on 18/Aug/21

let f (x) = x, we get fixed point x = - 1

so f (x) = 16 (x + 1) - 1

\Rightarrow (f \circ f) (x) = 16^{2} (x + 1) - 1

(f \circ f \circ f) (x) = 16^{3} (x + 1) - 1

(f \circ f \circ f \circ f) (x) = 16^{4} (x + 1) - 1

(\underset{n}{f \circ f \circ \dots \circ f}) (x) = 16^{n} (x + 1) - 1

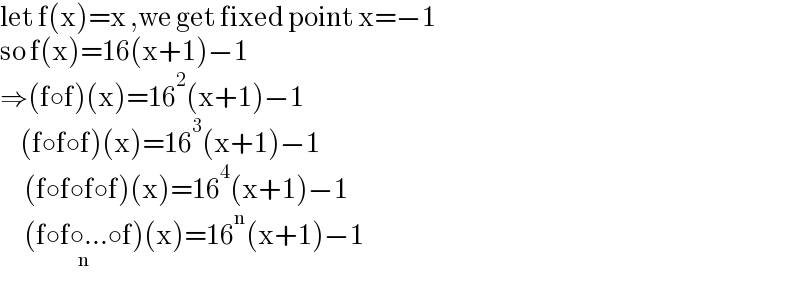
Commented by malwan last updated on 18/Aug/21

t h a n k y o u s i r

Commented by qaz last updated on 19/Aug/21

sorry . there is a error .

we need make a reverse iteration .

(f \circ f \circ f \circ f) (x) = 2^{4} (x + 1) - 1

\dots .

f (x) = 2 (x + 1) - 1 = 2 x + 1

Facebook Tweet Pin