Menu Close

If-f-tan-2-2-2-1-cos-find-f-sin-2-

Tinku Tara 0 Comments
Pin




Question Number 155527 by ZiYangLee last updated on 01/Oct/21
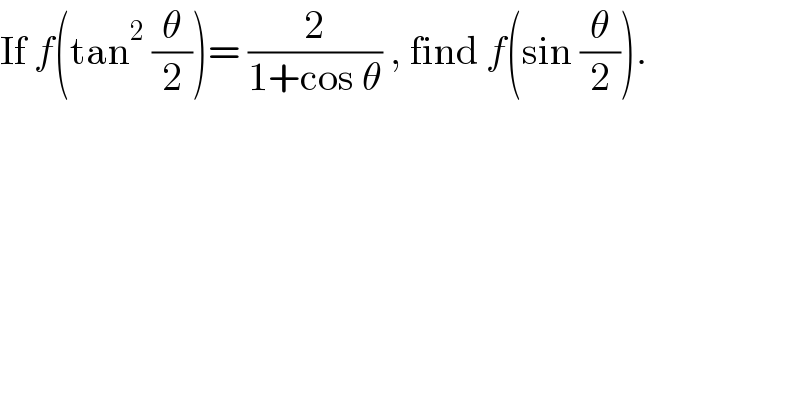
If f(tan^2 (θ/2))= (2/(1+cos θ)) , find f(sin (θ/2)).
$$\mathrm{If}\:{f}\left(\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\right)=\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{cos}\:\theta}\:,\:\mathrm{find}\:{f}\left(\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right). \\ $$
Answered by Ar Brandon last updated on 01/Oct/21
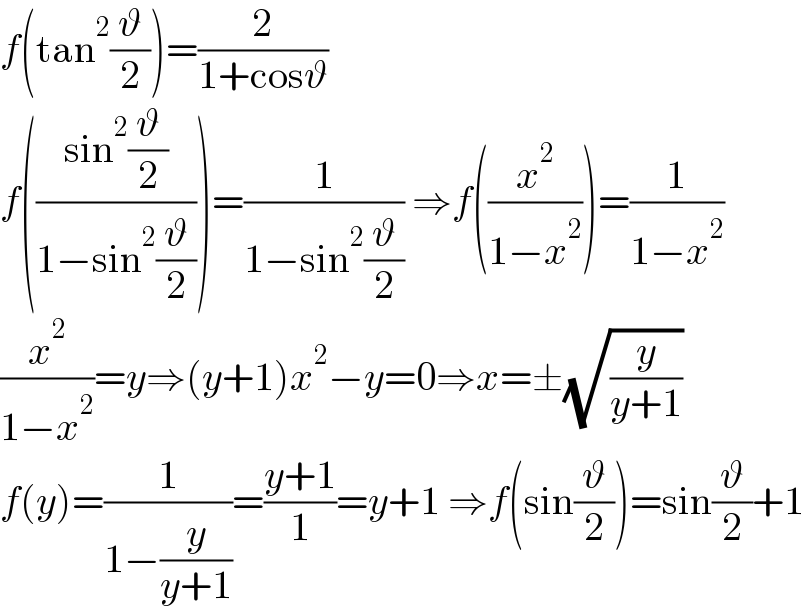
f(tan^2 (ϑ/2))=(2/(1+cosϑ)) f(((sin^2 (ϑ/2))/(1−sin^2 (ϑ/2))))=(1/(1−sin^2 (ϑ/2))) ⇒f((x^2 /(1−x^2 )))=(1/(1−x^2 )) (x^2 /(1−x^2 ))=y⇒(y+1)x^2 −y=0⇒x=±(√(y/(y+1))) f(y)=(1/(1−(y/(y+1))))=((y+1)/1)=y+1 ⇒f(sin(ϑ/2))=sin(ϑ/2)+1
$${f}\left(\mathrm{tan}^{\mathrm{2}} \frac{\vartheta}{\mathrm{2}}\right)=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{cos}\vartheta} \\ $$$${f}\left(\frac{\mathrm{sin}^{\mathrm{2}} \frac{\vartheta}{\mathrm{2}}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \frac{\vartheta}{\mathrm{2}}}\right)=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \frac{\vartheta}{\mathrm{2}}}\:\Rightarrow{f}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }={y}\Rightarrow\left({y}+\mathrm{1}\right){x}^{\mathrm{2}} −{y}=\mathrm{0}\Rightarrow{x}=\pm\sqrt{\frac{{y}}{{y}+\mathrm{1}}} \\ $$$${f}\left({y}\right)=\frac{\mathrm{1}}{\mathrm{1}−\frac{{y}}{{y}+\mathrm{1}}}=\frac{{y}+\mathrm{1}}{\mathrm{1}}={y}+\mathrm{1}\:\Rightarrow{f}\left(\mathrm{sin}\frac{\vartheta}{\mathrm{2}}\right)=\mathrm{sin}\frac{\vartheta}{\mathrm{2}}+\mathrm{1} \\ $$
Answered by mr W last updated on 02/Oct/21
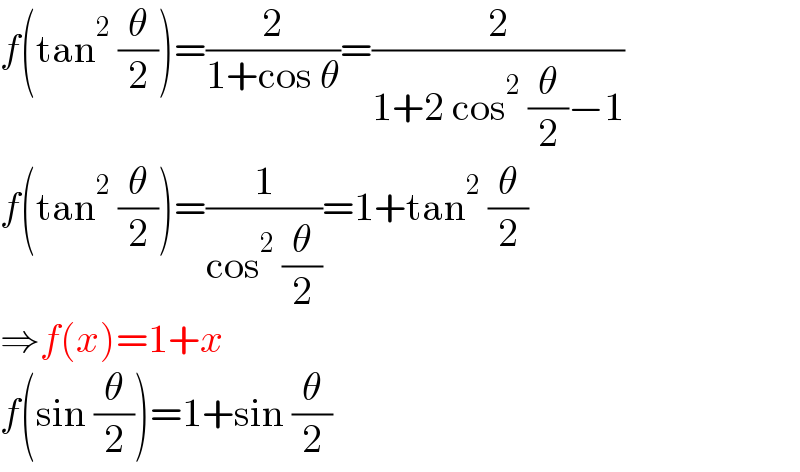
f(tan^2 (θ/2))=(2/(1+cos θ))=(2/(1+2 cos^2 (θ/2)−1)) f(tan^2 (θ/2))=(1/(cos^2 (θ/2)))=1+tan^2 (θ/2) ⇒f(x)=1+x f(sin (θ/2))=1+sin (θ/2)
$${f}\left(\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\right)=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{cos}\:\theta}=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}−\mathrm{1}} \\ $$$${f}\left(\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}=\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{1}+{x} \\ $$$${f}\left(\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right)=\mathrm{1}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *