if-f-x-1-f-x-3-and-f-25-72-find-f-2-

Question Number 157686 by MathSh last updated on 26/Oct/21

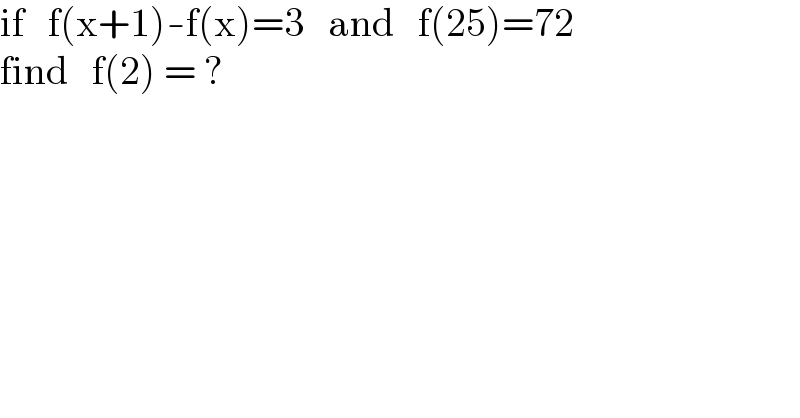
if f (x + 1) - f (x) = 3 and f (25) = 72

find f (2) = ?

Answered by tounghoungko last updated on 26/Oct/21

\Rightarrow f (x) = f (x + 1) - 3

\Rightarrow f (25) = f (24) - 3

\Rightarrow f (24) = f (23) - 3

⋮

\Rightarrow f (3) = f (2) - 3

- - - - - - - - - - -

\Rightarrow f (25) = 23 \times (- 3) + f (2)

\Rightarrow f (2) = 72 + 69 = 141

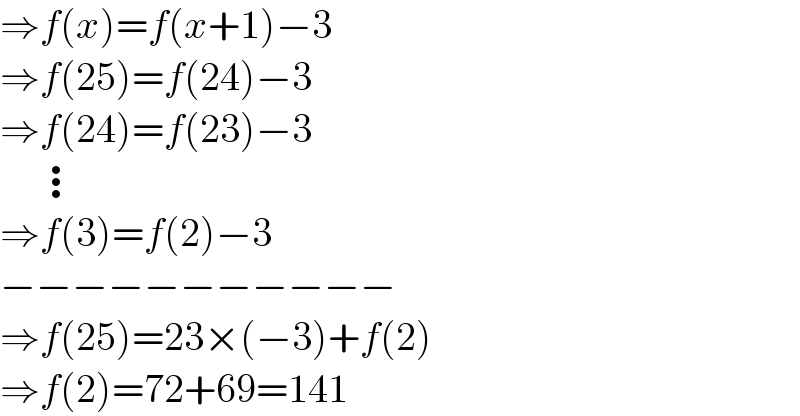
Answered by mr W last updated on 26/Oct/21

f (x + 1) = f (x) + 3

f (x + 2) = f (x + 1) + 3 = f (x) + 2 \times 3

\dots

f (x + n) = f (x) + 3 n

f (25) = f (2) + 3 (25 - 2)

f (2) = f (25) - 3 \times 23 = 72 - 3 \times 23 = 3

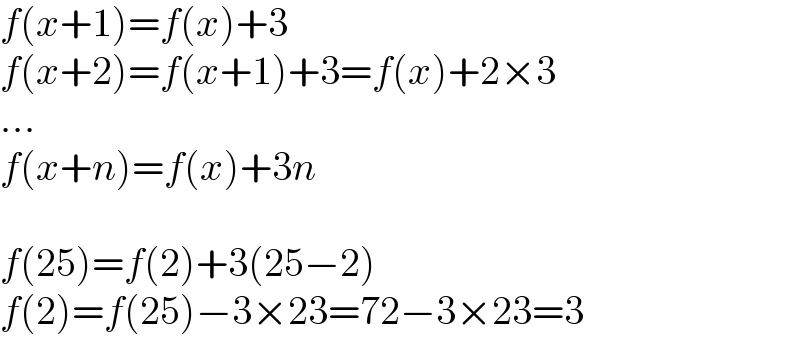
Commented by MathSh last updated on 26/Oct/21

Very nice dear S er, thank you so much

Answered by qaz last updated on 26/Oct/21

f (x + 1) - f (x) = 3

\underset{k = x}{\sum^{n}} (f (k + 1) - f (k)) = \underset{k = x}{\sum^{n}} 3

\Rightarrow f (n + 1) - f (x) = 3 (n + 1 - x)

f (25) - f (2) = 3 (25 - 2) = 69

\Rightarrow f (2) = 72 - 69 = 3

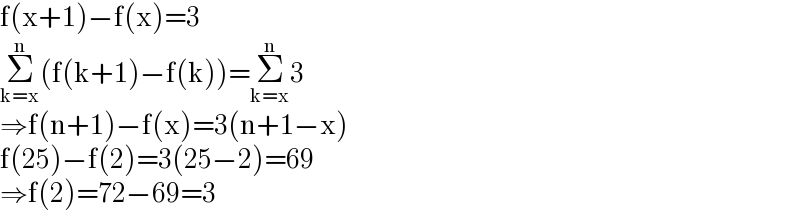
Commented by MathSh last updated on 26/Oct/21

Very nice dear S er, thank you so much

Facebook Tweet Pin