Question Number 92597 by john santu last updated on 08/May/20

$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}\:\mathrm{and}\:\mathrm{g}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}}\: \\ $$$$\mathrm{find}\:\mathrm{domain}\:\mathrm{and}\:\mathrm{range}\:\mathrm{of}\: \\ $$$$\mathrm{g}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\:. \\ $$
Commented by jagoll last updated on 08/May/20
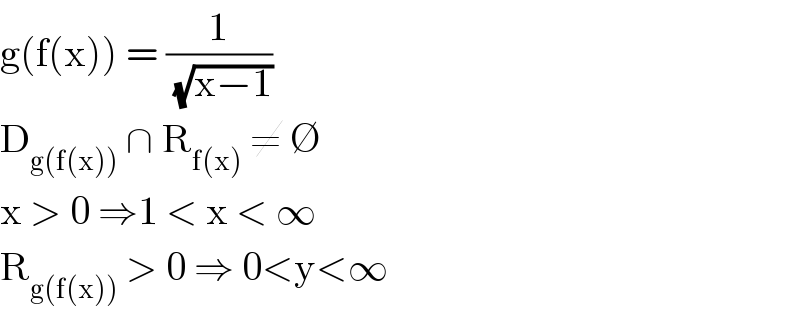
$$\mathrm{g}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}−\mathrm{1}}}\: \\ $$$$\mathrm{D}_{\mathrm{g}\left(\mathrm{f}\left(\mathrm{x}\right)\right)} \:\cap\:\mathrm{R}_{\mathrm{f}\left(\mathrm{x}\right)} \:\neq\:\varnothing \\ $$$$\mathrm{x}\:>\:\mathrm{0}\:\Rightarrow\mathrm{1}\:<\:\mathrm{x}\:<\:\infty\: \\ $$$$\mathrm{R}_{\mathrm{g}\left(\mathrm{f}\left(\mathrm{x}\right)\right)} \:>\:\mathrm{0}\:\Rightarrow\:\mathrm{0}<\mathrm{y}<\infty \\ $$
