Question Number 23922 by chernoaguero@gmail.com last updated on 09/Nov/17
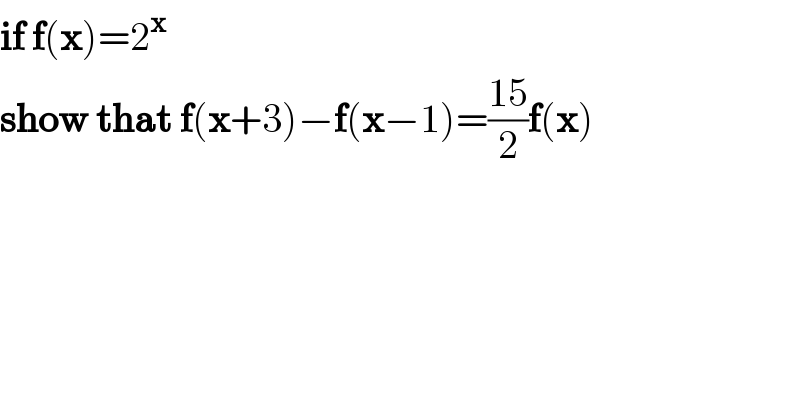
$$\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{2}^{\boldsymbol{\mathrm{x}}} \\ $$$$\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}+\mathrm{3}\right)−\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)=\frac{\mathrm{15}}{\mathrm{2}}\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right) \\ $$
Answered by $@ty@m last updated on 10/Nov/17

$${f}\left({x}+\mathrm{3}\right)=\mathrm{2}^{{x}+\mathrm{3}} =\mathrm{2}^{{x}} .\mathrm{2}^{\mathrm{3}} =\mathrm{8}.\mathrm{2}^{{x}} \\ $$$${f}\left({x}−\mathrm{1}\right)=\mathrm{2}^{{x}−\mathrm{1}} =\mathrm{2}^{{x}} .\mathrm{2}^{−\mathrm{1}} =\frac{\mathrm{2}^{{x}} }{\mathrm{2}} \\ $$$$\therefore{LHS}=\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}+\mathrm{3}\right)−\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{{x}} \left(\mathrm{8}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{15}}{\mathrm{2}}\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)={RHS} \\ $$
Commented by chernoaguero@gmail.com last updated on 10/Nov/17

$$\mathrm{Thank}\:\mathrm{u}\:\mathrm{sir}\:\mathrm{God}\:\mathrm{bless}\:\mathrm{u} \\ $$
