Question Number 120819 by bramlexs22 last updated on 03/Nov/20
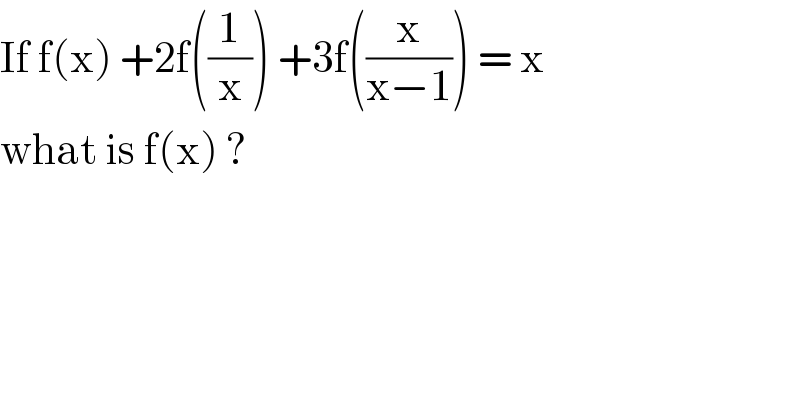
$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)\:+\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:+\mathrm{3f}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right)\:=\:\mathrm{x}\: \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{f}\left(\mathrm{x}\right)\:? \\ $$
Commented by liberty last updated on 03/Nov/20
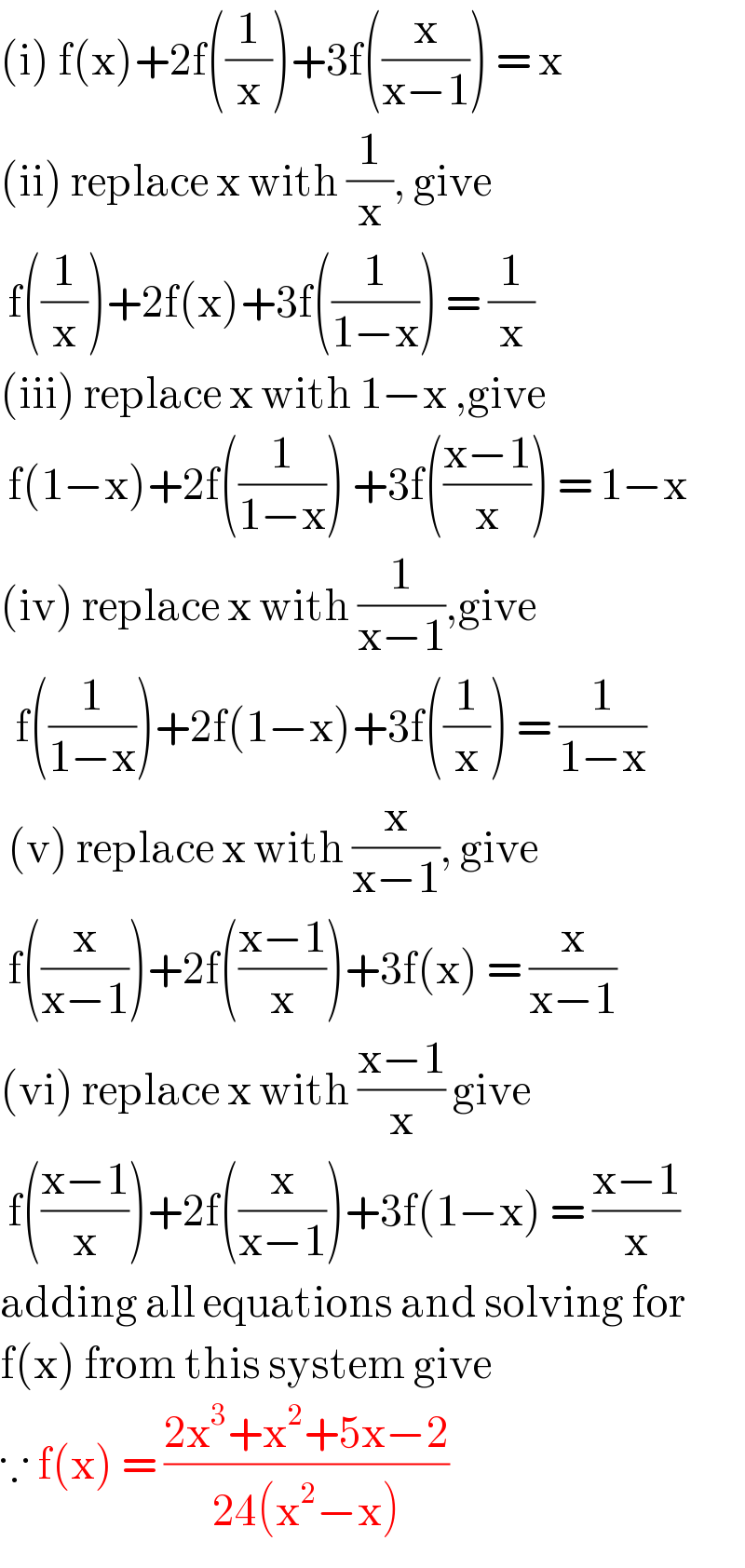
$$\left(\mathrm{i}\right)\:\mathrm{f}\left(\mathrm{x}\right)+\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{3f}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right)\:=\:\mathrm{x} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{replace}\:\mathrm{x}\:\mathrm{with}\:\frac{\mathrm{1}}{\mathrm{x}},\:\mathrm{give} \\ $$$$\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{2f}\left(\mathrm{x}\right)+\mathrm{3f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\left(\mathrm{iii}\right)\:\mathrm{replace}\:\mathrm{x}\:\mathrm{with}\:\mathrm{1}−\mathrm{x}\:,\mathrm{give} \\ $$$$\:\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right)+\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\:+\mathrm{3f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)\:=\:\mathrm{1}−\mathrm{x} \\ $$$$\left(\mathrm{iv}\right)\:\mathrm{replace}\:\mathrm{x}\:\mathrm{with}\:\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}},\mathrm{give}\: \\ $$$$\:\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)+\mathrm{2f}\left(\mathrm{1}−\mathrm{x}\right)+\mathrm{3f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}} \\ $$$$\:\left(\mathrm{v}\right)\:\mathrm{replace}\:\mathrm{x}\:\mathrm{with}\:\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}},\:\mathrm{give}\: \\ $$$$\:\mathrm{f}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right)+\mathrm{2f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)+\mathrm{3f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}} \\ $$$$\left(\mathrm{vi}\right)\:\mathrm{replace}\:\mathrm{x}\:\mathrm{with}\:\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\:\mathrm{give}\: \\ $$$$\:\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)+\mathrm{2f}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right)+\mathrm{3f}\left(\mathrm{1}−\mathrm{x}\right)\:=\:\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}} \\ $$$$\mathrm{adding}\:\mathrm{all}\:\mathrm{equations}\:\mathrm{and}\:\mathrm{solving}\:\mathrm{for}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{from}\:\mathrm{this}\:\mathrm{system}\:\mathrm{give}\: \\ $$$$\because\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{2x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{5x}−\mathrm{2}}{\mathrm{24}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)} \\ $$
Commented by bramlexs22 last updated on 03/Nov/20

$$\mathrm{great}… \\ $$
Commented by Ar Brandon last updated on 03/Nov/20
����
