Question Number 113904 by bobhans last updated on 16/Sep/20
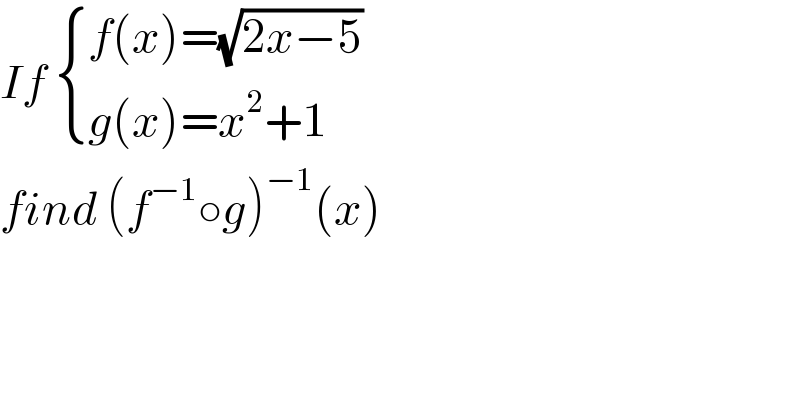
$${If}\:\begin{cases}{{f}\left({x}\right)=\sqrt{\mathrm{2}{x}−\mathrm{5}}}\\{{g}\left({x}\right)={x}^{\mathrm{2}} +\mathrm{1}}\end{cases} \\ $$$${find}\:\left({f}^{−\mathrm{1}} \circ{g}\right)^{−\mathrm{1}} \left({x}\right) \\ $$
Answered by bemath last updated on 16/Sep/20
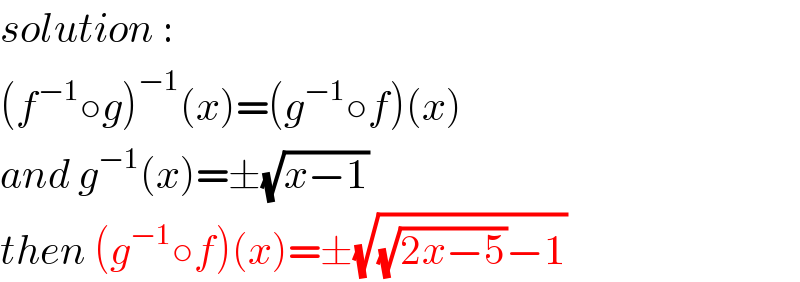
$${solution}\::\: \\ $$$$\left({f}^{−\mathrm{1}} \circ{g}\right)^{−\mathrm{1}} \left({x}\right)=\left({g}^{−\mathrm{1}} \circ{f}\right)\left({x}\right) \\ $$$${and}\:{g}^{−\mathrm{1}} \left({x}\right)=\pm\sqrt{{x}−\mathrm{1}} \\ $$$${then}\:\left({g}^{−\mathrm{1}} \circ{f}\right)\left({x}\right)=\pm\sqrt{\sqrt{\mathrm{2}{x}−\mathrm{5}}−\mathrm{1}} \\ $$
