Question Number 150469 by mathdanisur last updated on 12/Aug/21
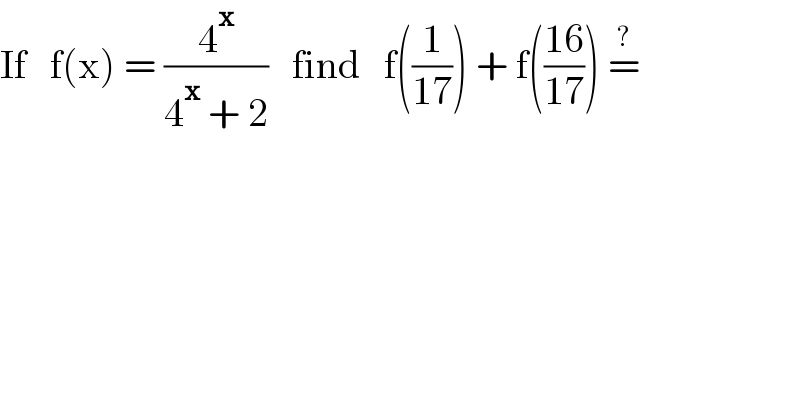
$$\mathrm{If}\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{4}^{\boldsymbol{\mathrm{x}}} }{\mathrm{4}^{\boldsymbol{\mathrm{x}}} \:+\:\mathrm{2}}\:\:\:\mathrm{find}\:\:\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{17}}\right)\:+\:\mathrm{f}\left(\frac{\mathrm{16}}{\mathrm{17}}\right)\:\overset{?} {=} \\ $$
Answered by gsk2684 last updated on 12/Aug/21
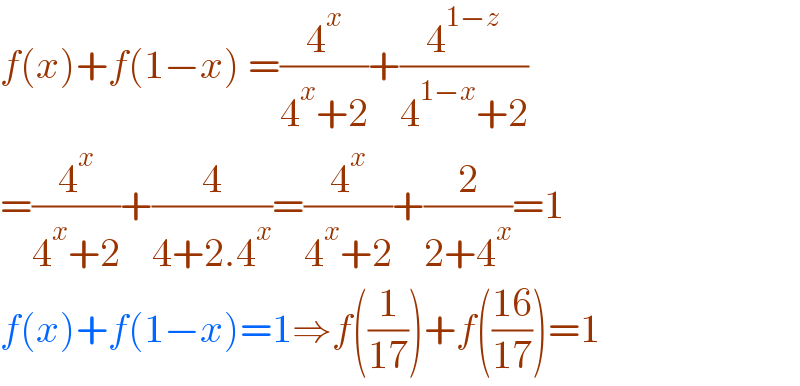
$${f}\left({x}\right)+{f}\left(\mathrm{1}−{x}\right)\:=\frac{\mathrm{4}^{{x}} }{\mathrm{4}^{{x}} +\mathrm{2}}+\frac{\mathrm{4}^{\mathrm{1}−{z}} }{\mathrm{4}^{\mathrm{1}−{x}} +\mathrm{2}} \\ $$$$=\frac{\mathrm{4}^{{x}} }{\mathrm{4}^{{x}} +\mathrm{2}}+\frac{\mathrm{4}}{\mathrm{4}+\mathrm{2}.\mathrm{4}^{{x}} }=\frac{\mathrm{4}^{{x}} }{\mathrm{4}^{{x}} +\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}+\mathrm{4}^{{x}} }=\mathrm{1} \\ $$$${f}\left({x}\right)+{f}\left(\mathrm{1}−{x}\right)=\mathrm{1}\Rightarrow{f}\left(\frac{\mathrm{1}}{\mathrm{17}}\right)+{f}\left(\frac{\mathrm{16}}{\mathrm{17}}\right)=\mathrm{1} \\ $$
Commented by mathdanisur last updated on 12/Aug/21

$$\mathrm{Thank}\:\mathrm{You}\:\mathrm{Ser} \\ $$
