Question Number 13099 by Joel577 last updated on 14/May/17

$$\mathrm{If}\:{f}\left({x}\:+\:\mathrm{5}\right)\:=\:{g}\left(\mathrm{2}{x}\:−\mathrm{1}\right) \\ $$$$\mathrm{Find}\:\mathrm{2}{f}^{−\mathrm{1}} \left({x}\right) \\ $$$$ \\ $$$$\left(\mathrm{A}\right)\:{g}^{−\mathrm{1}} \left({x}\right)\:+\:\mathrm{11}\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:{g}^{−\mathrm{1}} \left({x}/\mathrm{2}\right)\:+\:\mathrm{6} \\ $$$$\left(\mathrm{B}\right)\:{g}^{−\mathrm{1}} \left({x}\right)\:+\:\mathrm{9}\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{E}\right)\:{g}^{−\mathrm{1}} \left(\mathrm{2}{x}\right)\:+\:\mathrm{6} \\ $$$$\left(\mathrm{C}\right)\:{g}^{−\mathrm{1}} \left({x}\right)\:+\:\mathrm{6} \\ $$
Answered by 433 last updated on 14/May/17
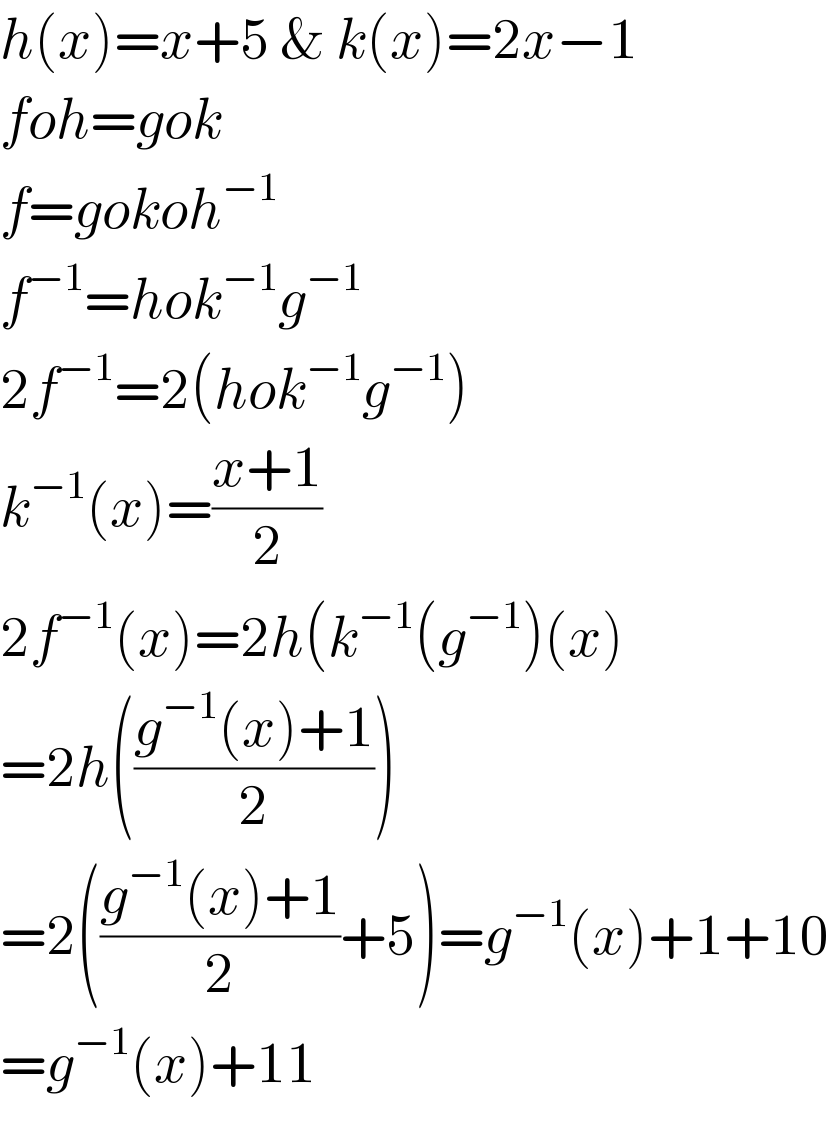
$${h}\left({x}\right)={x}+\mathrm{5}\:\&\:{k}\left({x}\right)=\mathrm{2}{x}−\mathrm{1} \\ $$$${foh}={gok} \\ $$$${f}={gokoh}^{−\mathrm{1}} \\ $$$${f}^{−\mathrm{1}} ={hok}^{−\mathrm{1}} {g}^{−\mathrm{1}} \\ $$$$\mathrm{2}{f}^{−\mathrm{1}} =\mathrm{2}\left({hok}^{−\mathrm{1}} {g}^{−\mathrm{1}} \right) \\ $$$${k}^{−\mathrm{1}} \left({x}\right)=\frac{{x}+\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}{f}^{−\mathrm{1}} \left({x}\right)=\mathrm{2}{h}\left({k}^{−\mathrm{1}} \left({g}^{−\mathrm{1}} \right)\left({x}\right)\right. \\ $$$$=\mathrm{2}{h}\left(\frac{{g}^{−\mathrm{1}} \left({x}\right)+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}\left(\frac{{g}^{−\mathrm{1}} \left({x}\right)+\mathrm{1}}{\mathrm{2}}+\mathrm{5}\right)={g}^{−\mathrm{1}} \left({x}\right)+\mathrm{1}+\mathrm{10} \\ $$$$={g}^{−\mathrm{1}} \left({x}\right)+\mathrm{11} \\ $$
Commented by Joel577 last updated on 15/May/17

$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by mrW1 last updated on 14/May/17

$${f}\left({x}\:+\:\mathrm{5}\right)\:=\:{g}\left(\mathrm{2}{x}\:−\mathrm{1}\right)={u} \\ $$$$\Rightarrow{x}+\mathrm{5}={f}^{−\mathrm{1}} \left({u}\right)\:\:\:\:\:…\left({i}\right) \\ $$$$\Rightarrow\mathrm{2}{x}−\mathrm{1}={g}^{−\mathrm{1}} \left({u}\right)\:\:\:…\left({ii}\right) \\ $$$$\mathrm{2}×\left({i}\right)−\left({ii}\right): \\ $$$$\Rightarrow\mathrm{11}=\mathrm{2}{f}^{−\mathrm{1}} \left({u}\right)−{g}^{−\mathrm{1}} \left({u}\right) \\ $$$$\Rightarrow\mathrm{2}{f}^{−\mathrm{1}} \left({u}\right)={g}^{−\mathrm{1}} \left({u}\right)+\mathrm{11} \\ $$$$\Rightarrow\mathrm{2}{f}^{−\mathrm{1}} \left({x}\right)={g}^{−\mathrm{1}} \left({x}\right)+\mathrm{11} \\ $$$$ \\ $$$$\Rightarrow{Answer}\:\left({A}\right) \\ $$
Commented by RasheedSindhi last updated on 14/May/17

$$\mathcal{E}\mathrm{asy}\:\mathrm{n}\:\mathrm{simple}! \\ $$
Commented by Joel577 last updated on 15/May/17

$${thank}\:{you}\:{very}\:{much} \\ $$
