Question Number 109546 by bemath last updated on 24/Aug/20
![If f(x) continue in [ 1,30] and ∫_6 ^(30) f(x)dx = 30, then ∫_1 ^9 f(3y+3)dy = __](https://www.tinkutara.com/question/Q109546.png)
$${If}\:{f}\left({x}\right)\:{continue}\:{in}\:\left[\:\mathrm{1},\mathrm{30}\right]\:{and}\: \\ $$$$\underset{\mathrm{6}} {\overset{\mathrm{30}} {\int}}{f}\left({x}\right){dx}\:=\:\mathrm{30},\:{then}\:\underset{\mathrm{1}} {\overset{\mathrm{9}} {\int}}{f}\left(\mathrm{3}{y}+\mathrm{3}\right){dy}\:=\:\_\_ \\ $$
Commented by kaivan.ahmadi last updated on 24/Aug/20
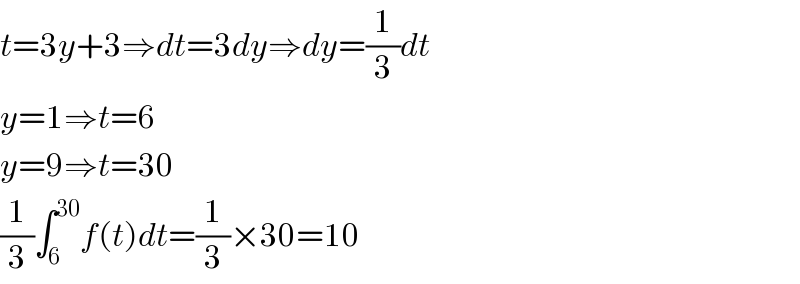
$${t}=\mathrm{3}{y}+\mathrm{3}\Rightarrow{dt}=\mathrm{3}{dy}\Rightarrow{dy}=\frac{\mathrm{1}}{\mathrm{3}}{dt} \\ $$$${y}=\mathrm{1}\Rightarrow{t}=\mathrm{6} \\ $$$${y}=\mathrm{9}\Rightarrow{t}=\mathrm{30} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{6}} ^{\mathrm{30}} {f}\left({t}\right){dt}=\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{30}=\mathrm{10} \\ $$
Commented by bemath last updated on 24/Aug/20

$${cooll}..{thanks} \\ $$
Answered by 1549442205PVT last updated on 24/Aug/20
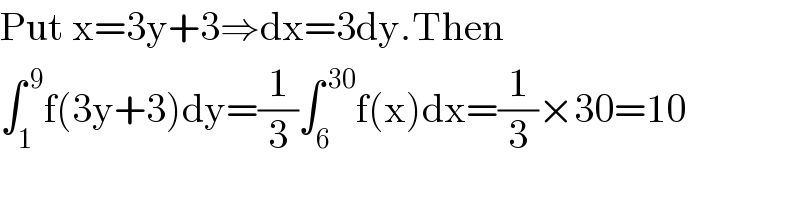
$$\mathrm{Put}\:\mathrm{x}=\mathrm{3y}+\mathrm{3}\Rightarrow\mathrm{dx}=\mathrm{3dy}.\mathrm{Then} \\ $$$$\int_{\mathrm{1}} ^{\:\mathrm{9}} \mathrm{f}\left(\mathrm{3y}+\mathrm{3}\right)\mathrm{dy}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{6}} ^{\:\mathrm{30}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{30}=\mathrm{10} \\ $$
