Menu Close

If-f-x-lim-x-x-n-x-n-x-n-x-n-x-gt-1-then-xf-x-ln-x-1-x-2-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 128540 by bramlexs22 last updated on 08/Jan/21
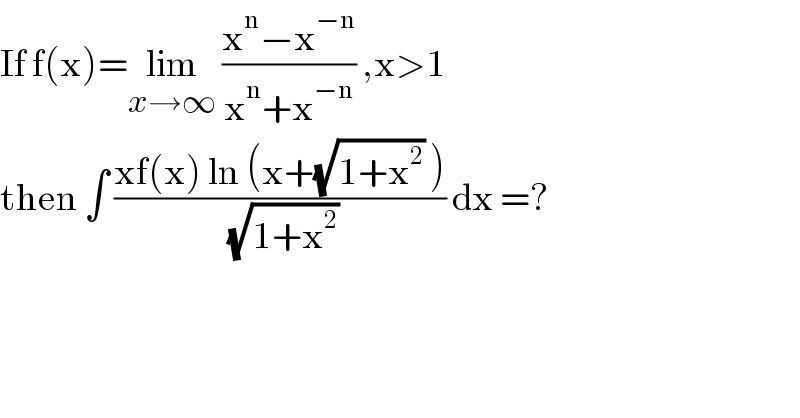
If f(x)=lim_(x→∞) ((x^n −x^(−n) )/(x^n +x^(−n) )) ,x>1 then ∫ ((xf(x) ln (x+(√(1+x^2 )) ))/( (√(1+x^2 )))) dx =?
$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{−\mathrm{n}} }{\mathrm{x}^{\mathrm{n}} +\mathrm{x}^{−\mathrm{n}} }\:,\mathrm{x}>\mathrm{1} \\ $$$$\mathrm{then}\:\int\:\frac{\mathrm{xf}\left(\mathrm{x}\right)\:\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\right)}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:=? \\ $$
Commented by liberty last updated on 08/Jan/21
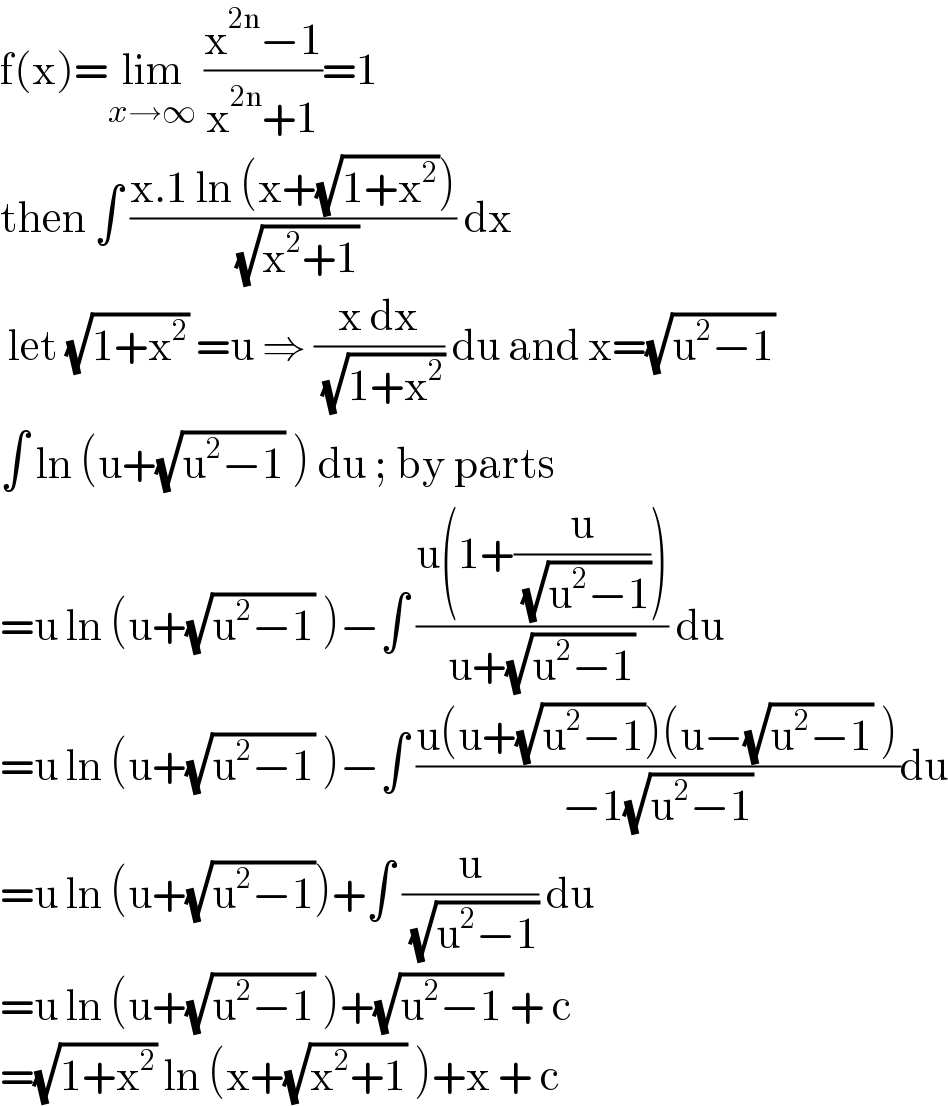
f(x)=lim_(x→∞) ((x^(2n) −1)/(x^(2n) +1))=1 then ∫ ((x.1 ln (x+(√(1+x^2 ))))/( (√(x^2 +1)))) dx let (√(1+x^2 )) =u ⇒ ((x dx)/( (√(1+x^2 )))) du and x=(√(u^2 −1)) ∫ ln (u+(√(u^2 −1)) ) du ; by parts =u ln (u+(√(u^2 −1)) )−∫ ((u(1+(u/( (√(u^2 −1))))))/(u+(√(u^2 −1)))) du =u ln (u+(√(u^2 −1)) )−∫ ((u(u+(√(u^2 −1)))(u−(√(u^2 −1)) ))/(−1(√(u^2 −1))))du =u ln (u+(√(u^2 −1)))+∫ (u/( (√(u^2 −1)))) du =u ln (u+(√(u^2 −1)) )+(√(u^2 −1)) + c =(√(1+x^2 )) ln (x+(√(x^2 +1)) )+x + c
$$\mathrm{f}\left(\mathrm{x}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{2n}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2n}} +\mathrm{1}}=\mathrm{1} \\ $$$$\mathrm{then}\:\int\:\frac{\mathrm{x}.\mathrm{1}\:\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\:\mathrm{dx}\: \\ $$$$\:\mathrm{let}\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\mathrm{u}\:\Rightarrow\:\frac{\mathrm{x}\:\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:\mathrm{du}\:\mathrm{and}\:\mathrm{x}=\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\int\:\mathrm{ln}\:\left(\mathrm{u}+\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:\right)\:\mathrm{du}\:;\:\mathrm{by}\:\mathrm{parts} \\ $$$$=\mathrm{u}\:\mathrm{ln}\:\left(\mathrm{u}+\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:\right)−\int\:\frac{\mathrm{u}\left(\mathrm{1}+\frac{\mathrm{u}}{\:\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}}\right)}{\mathrm{u}+\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}}\:\mathrm{du} \\ $$$$=\mathrm{u}\:\mathrm{ln}\:\left(\mathrm{u}+\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:\right)−\int\:\frac{\mathrm{u}\left(\mathrm{u}+\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\right)\left(\mathrm{u}−\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:\right)}{−\mathrm{1}\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}}\mathrm{du} \\ $$$$=\mathrm{u}\:\mathrm{ln}\:\left(\mathrm{u}+\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\right)+\int\:\frac{\mathrm{u}}{\:\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}}\:\mathrm{du} \\ $$$$=\mathrm{u}\:\mathrm{ln}\:\left(\mathrm{u}+\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:\right)+\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:+\:\mathrm{c} \\ $$$$=\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\right)+\mathrm{x}\:+\:\mathrm{c} \\ $$
Answered by mathmax by abdo last updated on 10/Jan/21
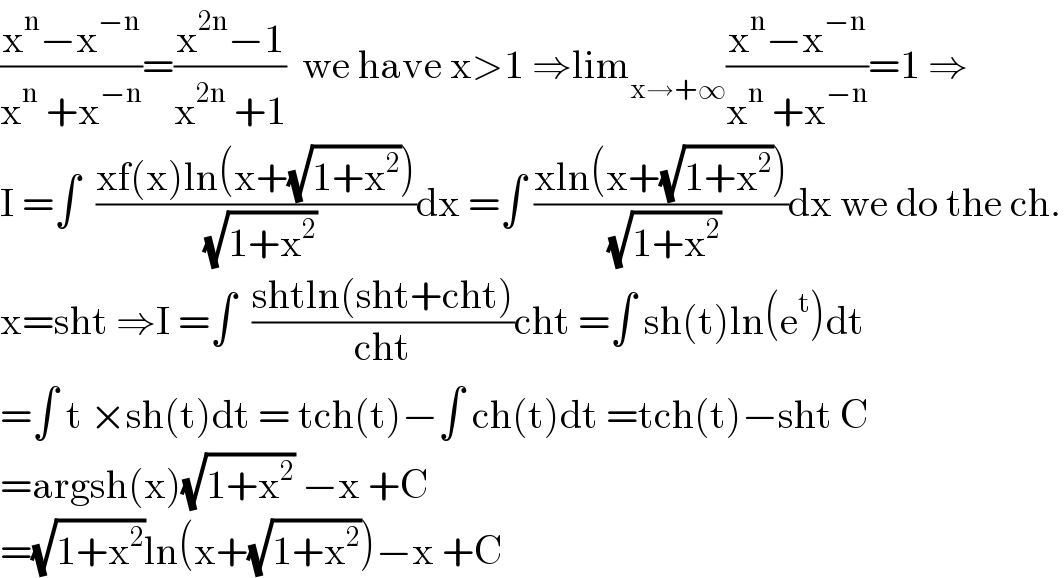
((x^n −x^(−n) )/(x^n +x^(−n) ))=((x^(2n) −1)/(x^(2n) +1)) we have x>1 ⇒lim_(x→+∞) ((x^n −x^(−n) )/(x^n +x^(−n) ))=1 ⇒ I =∫ ((xf(x)ln(x+(√(1+x^2 ))))/( (√(1+x^2 ))))dx =∫ ((xln(x+(√(1+x^2 ))))/( (√(1+x^2 ))))dx we do the ch. x=sht ⇒I =∫ ((shtln(sht+cht))/(cht))cht =∫ sh(t)ln(e^t )dt =∫ t ×sh(t)dt = tch(t)−∫ ch(t)dt =tch(t)−sht C =argsh(x)(√(1+x^2 )) −x +C =(√(1+x^2 ))ln(x+(√(1+x^2 )))−x +C
$$\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{−\mathrm{n}} }{\mathrm{x}^{\mathrm{n}} \:+\mathrm{x}^{−\mathrm{n}} }=\frac{\mathrm{x}^{\mathrm{2n}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2n}} \:+\mathrm{1}}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{x}>\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \frac{\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{−\mathrm{n}} }{\mathrm{x}^{\mathrm{n}} \:+\mathrm{x}^{−\mathrm{n}} }=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{xf}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:=\int\:\frac{\mathrm{xln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{ch}. \\ $$$$\mathrm{x}=\mathrm{sht}\:\Rightarrow\mathrm{I}\:=\int\:\:\frac{\mathrm{shtln}\left(\mathrm{sht}+\mathrm{cht}\right)}{\mathrm{cht}}\mathrm{cht}\:=\int\:\mathrm{sh}\left(\mathrm{t}\right)\mathrm{ln}\left(\mathrm{e}^{\mathrm{t}} \right)\mathrm{dt} \\ $$$$=\int\:\mathrm{t}\:×\mathrm{sh}\left(\mathrm{t}\right)\mathrm{dt}\:=\:\mathrm{tch}\left(\mathrm{t}\right)−\int\:\mathrm{ch}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{tch}\left(\mathrm{t}\right)−\mathrm{sht}\:\mathrm{C} \\ $$$$=\mathrm{argsh}\left(\mathrm{x}\right)\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:−\mathrm{x}\:+\mathrm{C} \\ $$$$=\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)−\mathrm{x}\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *