if-f-x-log-1-2ax-log-1-bx-x-x-0-k-x-0-is-continuous-at-x-0-then-k-

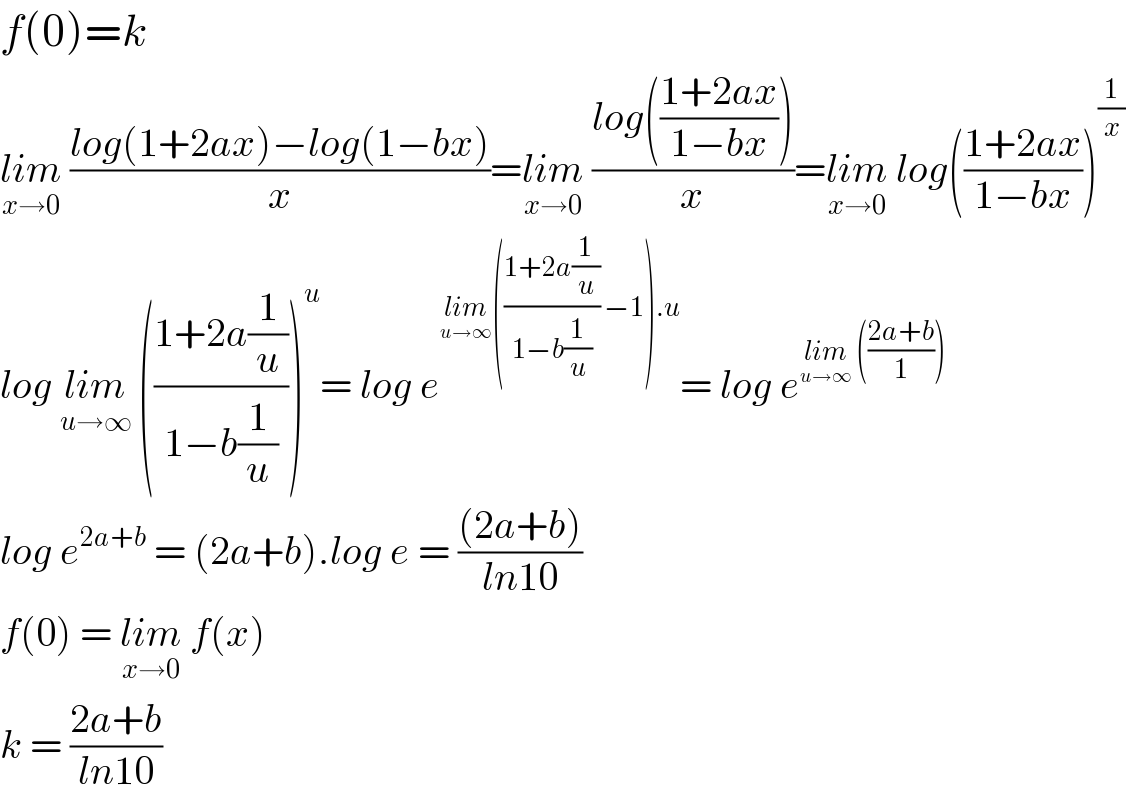
Question Number 63922 by raj last updated on 11/Jul/19

if f (x) = {\begin{cases} \frac{\log (1 + 2 a x) - \log (1 - b x)}{x} & x \neq 0 \\ k & x = 0 \end{cases}

is continuous at x = 0 then k = ?

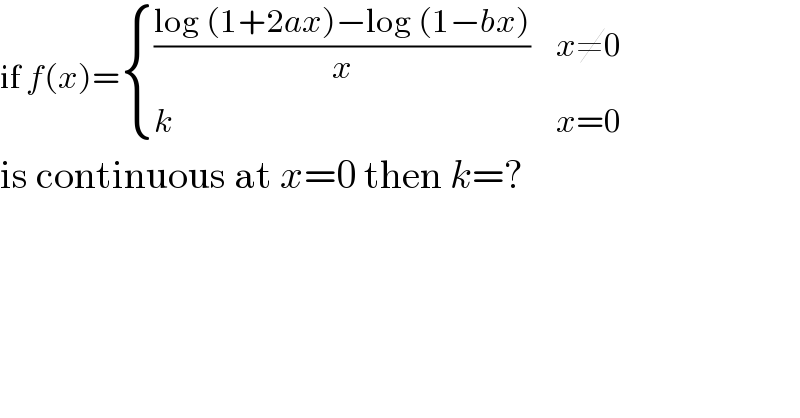
Commented by kaivan.ahmadi last updated on 11/Jul/19

{l i m}_{x \to 0} f (x) \overset{h o p}{=} {l i m}_{x \to 0} \frac{2 a}{l n 10 \times (1 + 2 a x)} - \frac{- b}{l n 10 \times (1 - b x)} =

\frac{2 a}{l n 10} + \frac{b}{l n 10} = \frac{2 a + b}{l n 10}

k = f (0) = {l i m}_{x \to 0} f (x) = \frac{2 a + b}{l n 10}

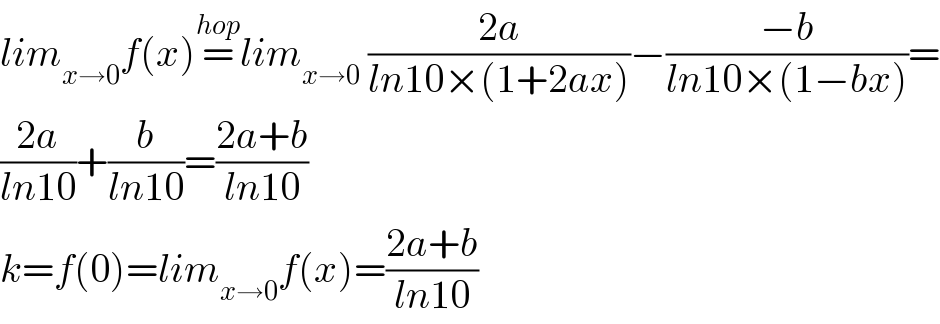
Commented by mathmax by abdo last updated on 12/Jul/19

a t V (0) l o g (1 + 2 a x) \sim \frac{2 a x}{l n (10)} a n d l o g (1 - b x) \sim \frac{- b x}{l n (10)} \Rightarrow

\frac{l o g (1 + 2 a x) - l o g (1 - b x)}{x} \sim \frac{2 a x + b x}{x l n (10)} = \frac{2 a + b}{l n (10)}

f c o n t i n u e a t x_{0} = 0 \Rightarrow {l i m}_{x \to 0} f (x) = f (0) = k \Rightarrow k = \frac{2 a + b}{l n (10)}

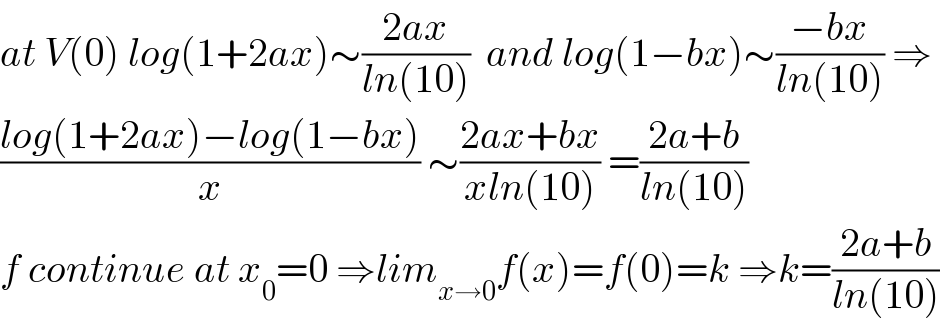
Commented by raj last updated on 11/Jul/19

t h a n k y o u

Commented by Mikael last updated on 11/Jul/19

f (0) = k

\underset{x \to 0}{l i m} \frac{l o g (1 + 2 a x) - l o g (1 - b x)}{x} = \underset{x \to 0}{l i m} \frac{l o g (\frac{1 + 2 a x}{1 - b x})}{x} = \underset{x \to 0}{l i m} l o g {(\frac{1 + 2 a x}{1 - b x})}^{\frac{1}{x}}

l o g \underset{u \to \infty}{l i m} {(\frac{1 + 2 a \frac{1}{u}}{1 - b \frac{1}{u}})}^{u} = l o g e^{\underset{u \to \infty}{l i m} (\frac{1 + 2 a \frac{1}{u}}{1 - b \frac{1}{u}} - 1) . u} = l o g e^{\underset{u \to \infty}{l i m} (\frac{2 a + b}{1})}

l o g e^{2 a + b} = (2 a + b) . l o g e = \frac{(2 a + b)}{l n 10}

f (0) = \underset{x \to 0}{l i m} f (x)

k = \frac{2 a + b}{l n 10}

Facebook Tweet Pin