Question Number 106217 by bobhans last updated on 03/Aug/20
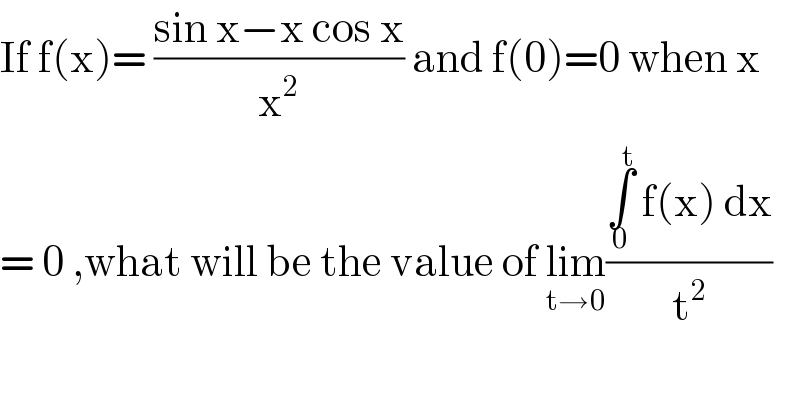
$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)=\:\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\:\mathrm{and}\:\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}\:\mathrm{when}\:\mathrm{x} \\ $$$$=\:\mathrm{0}\:,\mathrm{what}\:\mathrm{will}\:\mathrm{be}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\underset{\mathrm{0}} {\overset{\mathrm{t}} {\int}}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}}{\mathrm{t}^{\mathrm{2}} } \\ $$$$ \\ $$
Answered by john santu last updated on 03/Aug/20
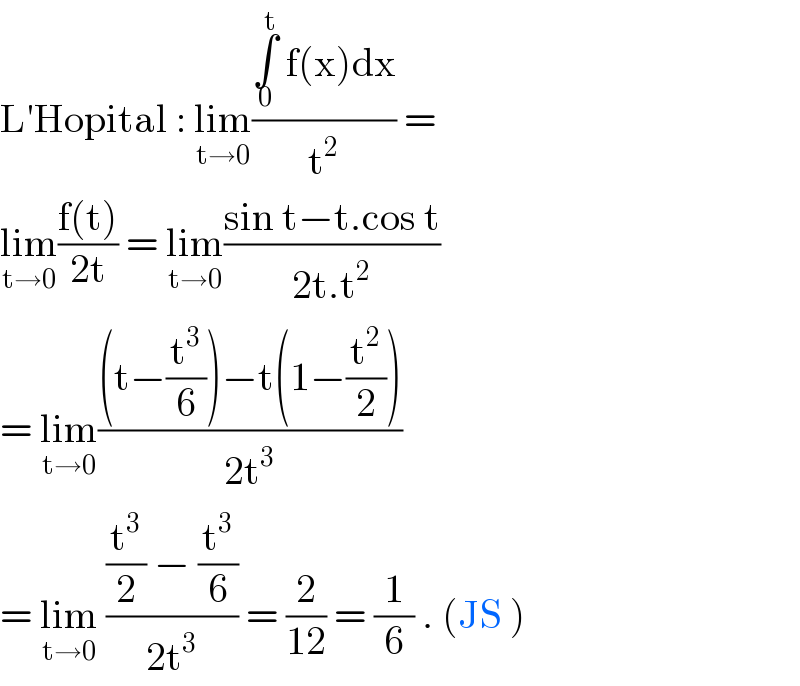
$$\mathrm{L}'\mathrm{Hopital}\::\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\underset{\mathrm{0}} {\overset{\mathrm{t}} {\int}}\:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}}{\mathrm{t}^{\mathrm{2}} }\:= \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{f}\left(\mathrm{t}\right)}{\mathrm{2t}}\:=\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{t}−\mathrm{t}.\mathrm{cos}\:\mathrm{t}}{\mathrm{2t}.\mathrm{t}^{\mathrm{2}} } \\ $$$$=\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{t}−\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{6}}\right)−\mathrm{t}\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)}{\mathrm{2t}^{\mathrm{3}} }\: \\ $$$$=\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{2}}\:−\:\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{2t}^{\mathrm{3}} }\:=\:\frac{\mathrm{2}}{\mathrm{12}}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\:.\:\left(\mathrm{JS}\:\right) \\ $$
