Menu Close

If-f-x-x-4-ax-3-bx-2-cx-d-f-1-5-f-2-10-f-3-15-find-f-9-f-5-

Tinku Tara 0 Comments
Pin




Question Number 120706 by ZiYangLee last updated on 02/Nov/20
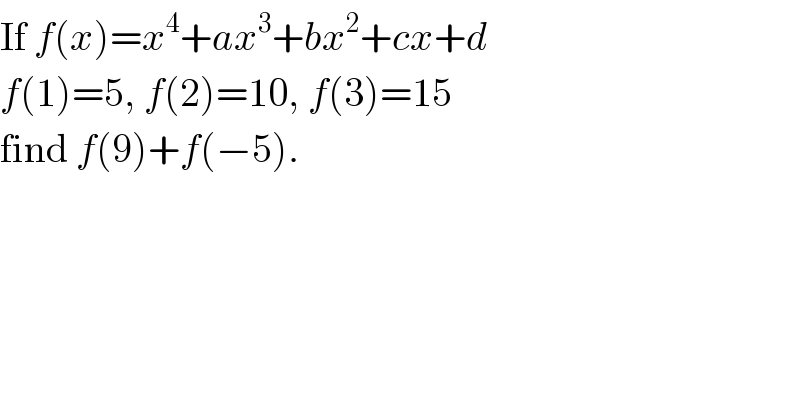
If f(x)=x^4 +ax^3 +bx^2 +cx+d f(1)=5, f(2)=10, f(3)=15 find f(9)+f(−5).
$$\mathrm{If}\:{f}\left({x}\right)={x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{5},\:{f}\left(\mathrm{2}\right)=\mathrm{10},\:{f}\left(\mathrm{3}\right)=\mathrm{15} \\ $$$$\mathrm{find}\:{f}\left(\mathrm{9}\right)+{f}\left(−\mathrm{5}\right). \\ $$
Commented by liberty last updated on 02/Nov/20
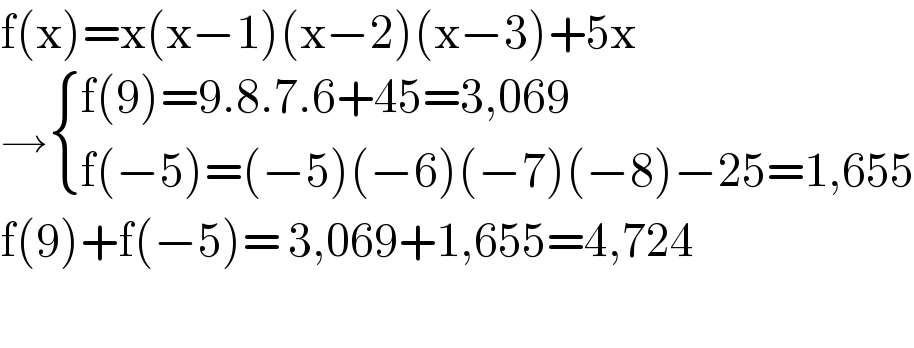
f(x)=x(x−1)(x−2)(x−3)+5x → { ((f(9)=9.8.7.6+45=3,069)),((f(−5)=(−5)(−6)(−7)(−8)−25=1,655)) :} f(9)+f(−5)= 3,069+1,655=4,724
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)+\mathrm{5x} \\ $$$$\rightarrow\begin{cases}{\mathrm{f}\left(\mathrm{9}\right)=\mathrm{9}.\mathrm{8}.\mathrm{7}.\mathrm{6}+\mathrm{45}=\mathrm{3},\mathrm{069}}\\{\mathrm{f}\left(−\mathrm{5}\right)=\left(−\mathrm{5}\right)\left(−\mathrm{6}\right)\left(−\mathrm{7}\right)\left(−\mathrm{8}\right)−\mathrm{25}=\mathrm{1},\mathrm{655}}\end{cases} \\ $$$$\mathrm{f}\left(\mathrm{9}\right)+\mathrm{f}\left(−\mathrm{5}\right)=\:\mathrm{3},\mathrm{069}+\mathrm{1},\mathrm{655}=\mathrm{4},\mathrm{724} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *