If-for-positive-integers-a-and-b-a-b-a-b-b-a-find-a-2-b-2-

Question Number 16990 by 1234Hello last updated on 29/Jun/17

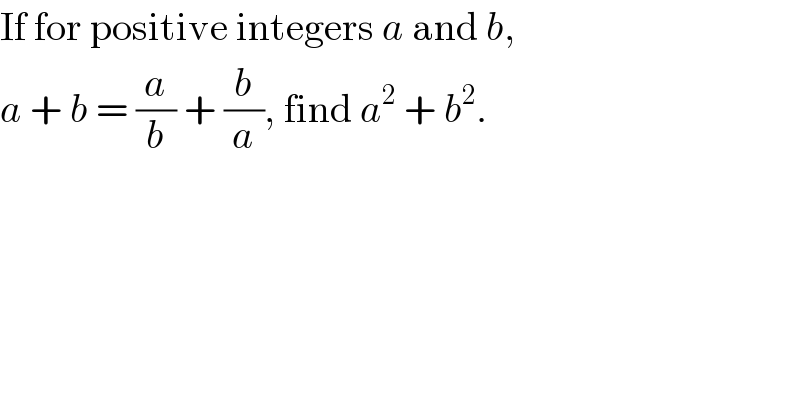
$$\mathrm{If}\:\mathrm{for}\:\mathrm{positive}\:\mathrm{integers}\:{a}\:\mathrm{and}\:{b}, \\ $$$${a}\:+\:{b}\:=\:\frac{{a}}{{b}}\:+\:\frac{{b}}{{a}},\:\mathrm{find}\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} . \\ $$

Commented by RasheedSoomro last updated on 29/Jun/17

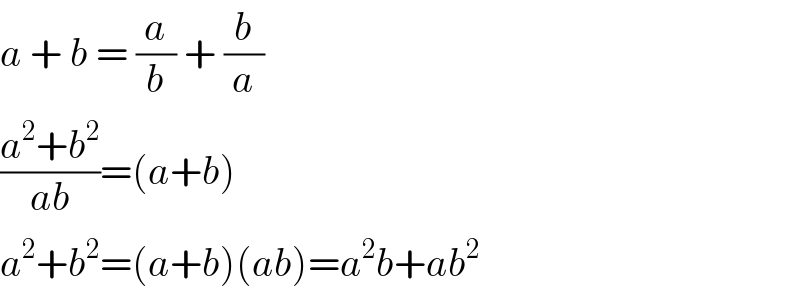
a + b = (a/b) + (b/a) ((a^2 +b^2 )/(ab))=(a+b) a^2 +b^2 =(a+b)(ab)=a^2 b+ab^2

$${a}\:+\:{b}\:=\:\frac{{a}}{{b}}\:+\:\frac{{b}}{{a}} \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{ab}}=\left({a}+{b}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left({a}+{b}\right)\left({ab}\right)={a}^{\mathrm{2}} {b}+{ab}^{\mathrm{2}} \\ $$

Commented by 1234Hello last updated on 29/Jun/17

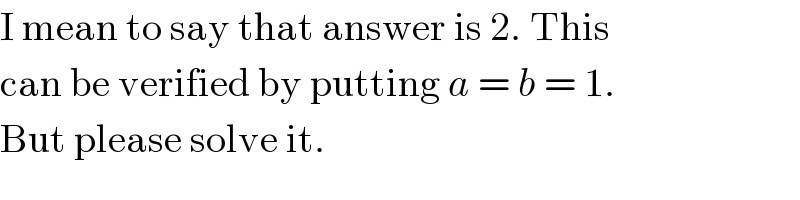
I mean to say that answer is 2. This can be verified by putting a = b = 1. But please solve it.

$$\mathrm{I}\:\mathrm{mean}\:\mathrm{to}\:\mathrm{say}\:\mathrm{that}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{2}.\:\mathrm{This} \\ $$$$\mathrm{can}\:\mathrm{be}\:\mathrm{verified}\:\mathrm{by}\:\mathrm{putting}\:{a}\:=\:{b}\:=\:\mathrm{1}. \\ $$$$\mathrm{But}\:\mathrm{please}\:\mathrm{solve}\:\mathrm{it}. \\ $$

Commented by RasheedSoomro last updated on 29/Jun/17

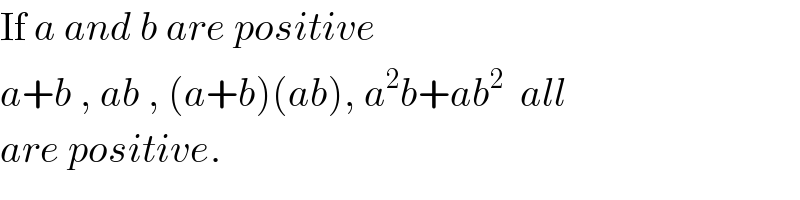
If a and b are positive a+b , ab , (a+b)(ab), a^2 b+ab^2 all are positive.

$$\mathrm{If}\:{a}\:{and}\:{b}\:{are}\:{positive} \\ $$$${a}+{b}\:,\:{ab}\:,\:\left({a}+{b}\right)\left({ab}\right),\:{a}^{\mathrm{2}} {b}+{ab}^{\mathrm{2}} \:\:{all} \\ $$$${are}\:{positive}. \\ $$

Commented by RasheedSoomro last updated on 29/Jun/17

I now understand the question! But the solution is difficult.

$$\mathrm{I}\:\mathrm{now}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{question}! \\ $$$$\mathrm{But}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{difficult}. \\ $$

Answered by mrW1 last updated on 29/Jun/17

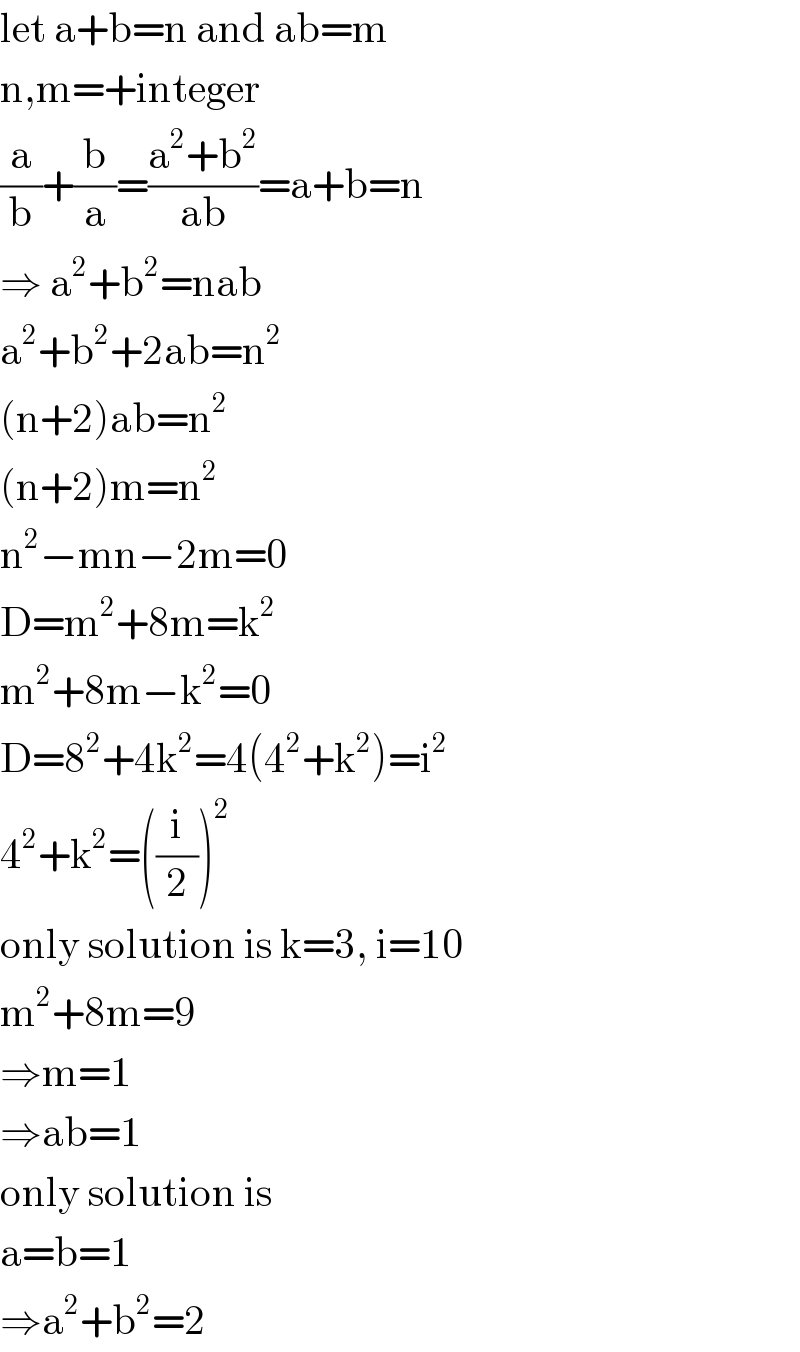
let a+b=n and ab=m n,m=+integer (a/b)+(b/a)=((a^2 +b^2 )/(ab))=a+b=n ⇒ a^2 +b^2 =nab a^2 +b^2 +2ab=n^2 (n+2)ab=n^2 (n+2)m=n^2 n^2 −mn−2m=0 D=m^2 +8m=k^2 m^2 +8m−k^2 =0 D=8^2 +4k^2 =4(4^2 +k^2 )=i^2 4^2 +k^2 =((i/2))^2 only solution is k=3, i=10 m^2 +8m=9 ⇒m=1 ⇒ab=1 only solution is a=b=1 ⇒a^2 +b^2 =2

$$\mathrm{let}\:\mathrm{a}+\mathrm{b}=\mathrm{n}\:\mathrm{and}\:\mathrm{ab}=\mathrm{m} \\ $$$$\mathrm{n},\mathrm{m}=+\mathrm{integer} \\ $$$$\frac{\mathrm{a}}{\mathrm{b}}+\frac{\mathrm{b}}{\mathrm{a}}=\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{ab}}=\mathrm{a}+\mathrm{b}=\mathrm{n} \\ $$$$\Rightarrow\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{nab} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2ab}=\mathrm{n}^{\mathrm{2}} \\ $$$$\left(\mathrm{n}+\mathrm{2}\right)\mathrm{ab}=\mathrm{n}^{\mathrm{2}} \\ $$$$\left(\mathrm{n}+\mathrm{2}\right)\mathrm{m}=\mathrm{n}^{\mathrm{2}} \\ $$$$\mathrm{n}^{\mathrm{2}} −\mathrm{mn}−\mathrm{2m}=\mathrm{0} \\ $$$$\mathrm{D}=\mathrm{m}^{\mathrm{2}} +\mathrm{8m}=\mathrm{k}^{\mathrm{2}} \\ $$$$\mathrm{m}^{\mathrm{2}} +\mathrm{8m}−\mathrm{k}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{D}=\mathrm{8}^{\mathrm{2}} +\mathrm{4k}^{\mathrm{2}} =\mathrm{4}\left(\mathrm{4}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} \right)=\mathrm{i}^{\mathrm{2}} \\ $$$$\mathrm{4}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} =\left(\frac{\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{only}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{k}=\mathrm{3},\:\mathrm{i}=\mathrm{10} \\ $$$$\mathrm{m}^{\mathrm{2}} +\mathrm{8m}=\mathrm{9} \\ $$$$\Rightarrow\mathrm{m}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{ab}=\mathrm{1} \\ $$$$\mathrm{only}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{a}=\mathrm{b}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{2} \\ $$

Commented by Tinkutara last updated on 29/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Commented by RasheedSoomro last updated on 29/Jun/17

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{sir}! \\ $$

Facebook Tweet Pin

If-for-positive-integers-a-and-b-a-b-a-b-b-a-find-a-2-b-2-

Leave a Reply Cancel reply