Question Number 81591 by john santu last updated on 14/Feb/20
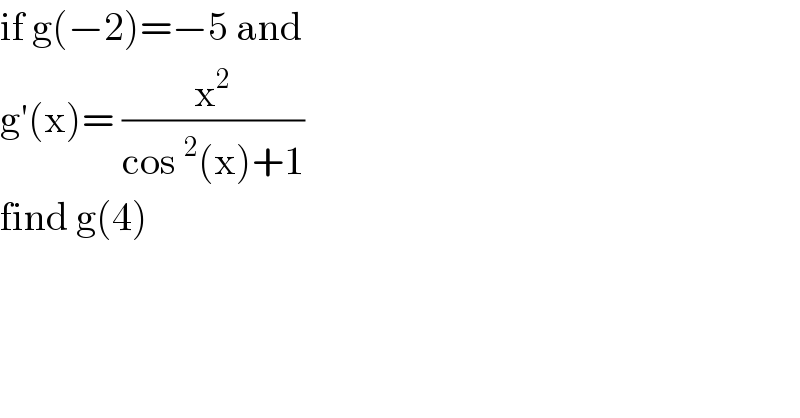
$$\mathrm{if}\:\mathrm{g}\left(−\mathrm{2}\right)=−\mathrm{5}\:\mathrm{and}\: \\ $$$$\mathrm{g}'\left(\mathrm{x}\right)=\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{1}} \\ $$$$\mathrm{find}\:\mathrm{g}\left(\mathrm{4}\right)\: \\ $$
Commented by mr W last updated on 14/Feb/20
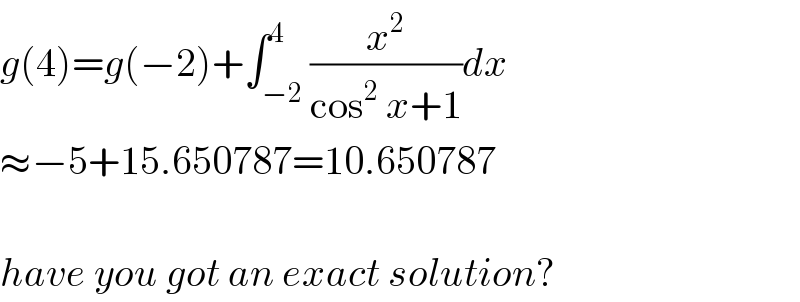
$${g}\left(\mathrm{4}\right)={g}\left(−\mathrm{2}\right)+\int_{−\mathrm{2}} ^{\mathrm{4}} \frac{{x}^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:{x}+\mathrm{1}}{dx} \\ $$$$\approx−\mathrm{5}+\mathrm{15}.\mathrm{650787}=\mathrm{10}.\mathrm{650787} \\ $$$$ \\ $$$${have}\:{you}\:{got}\:{an}\:{exact}\:{solution}? \\ $$
Commented by john santu last updated on 14/Feb/20
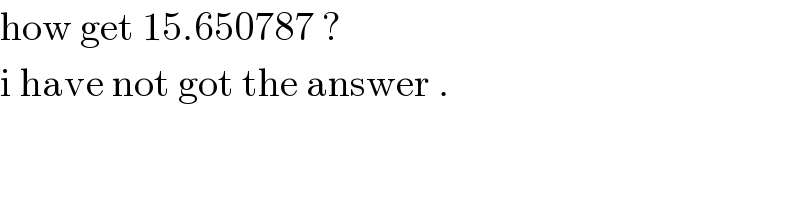
$$\mathrm{how}\:\mathrm{get}\:\mathrm{15}.\mathrm{650787}\:? \\ $$$$\mathrm{i}\:\mathrm{have}\:\mathrm{not}\:\mathrm{got}\:\mathrm{the}\:\mathrm{answer}\:. \\ $$
Commented by mr W last updated on 14/Feb/20

Commented by john santu last updated on 14/Feb/20
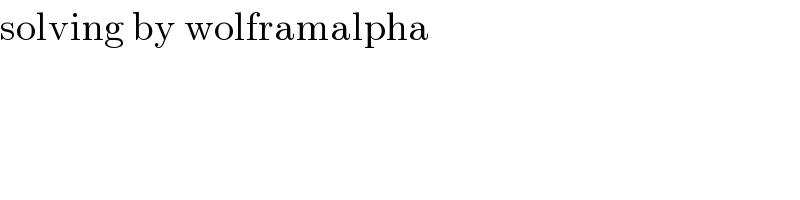
$$\mathrm{solving}\:\mathrm{by}\:\mathrm{wolframalpha} \\ $$
Commented by mr W last updated on 14/Feb/20
$${yes}.\:{for}\:{numerical}\:{integral}\:{there}\:{are} \\ $$$${many}\:{tools}.\:{nobody}\:{calculates}\:{by}\:{hand}. \\ $$
Commented by mathmax by abdo last updated on 14/Feb/20
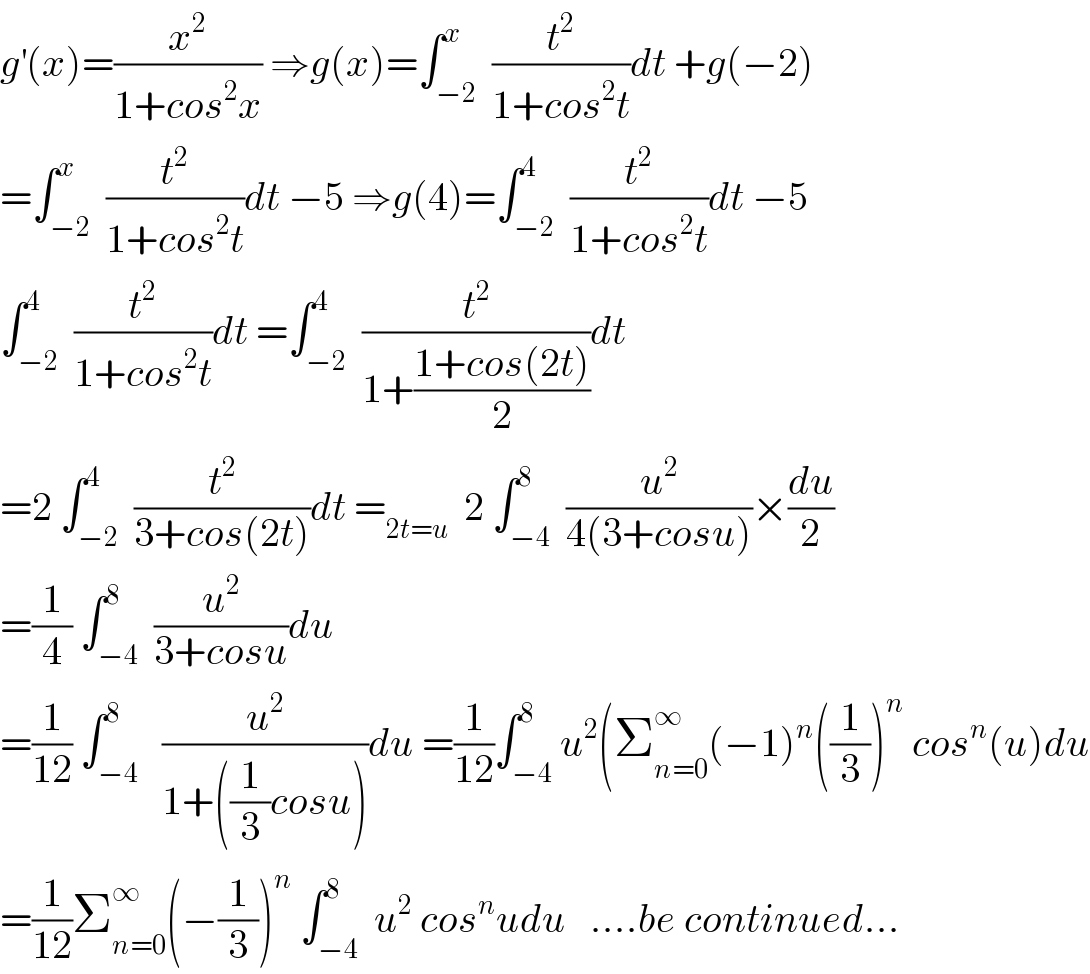
$${g}^{'} \left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{cos}^{\mathrm{2}} {x}}\:\Rightarrow{g}\left({x}\right)=\int_{−\mathrm{2}} ^{{x}} \:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{cos}^{\mathrm{2}} {t}}{dt}\:+{g}\left(−\mathrm{2}\right) \\ $$$$=\int_{−\mathrm{2}} ^{{x}} \:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{cos}^{\mathrm{2}} {t}}{dt}\:−\mathrm{5}\:\Rightarrow{g}\left(\mathrm{4}\right)=\int_{−\mathrm{2}} ^{\mathrm{4}} \:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{cos}^{\mathrm{2}} {t}}{dt}\:−\mathrm{5} \\ $$$$\int_{−\mathrm{2}} ^{\mathrm{4}} \:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{cos}^{\mathrm{2}} {t}}{dt}\:=\int_{−\mathrm{2}} ^{\mathrm{4}} \:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}{dt} \\ $$$$=\mathrm{2}\:\int_{−\mathrm{2}} ^{\mathrm{4}} \:\frac{{t}^{\mathrm{2}} }{\mathrm{3}+{cos}\left(\mathrm{2}{t}\right)}{dt}\:=_{\mathrm{2}{t}={u}} \:\:\mathrm{2}\:\int_{−\mathrm{4}} ^{\mathrm{8}} \:\frac{{u}^{\mathrm{2}} }{\mathrm{4}\left(\mathrm{3}+{cosu}\right)}×\frac{{du}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{−\mathrm{4}} ^{\mathrm{8}} \:\frac{{u}^{\mathrm{2}} }{\mathrm{3}+{cosu}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\:\int_{−\mathrm{4}} ^{\mathrm{8}} \:\:\frac{{u}^{\mathrm{2}} }{\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{3}}{cosu}\right)}{du}\:=\frac{\mathrm{1}}{\mathrm{12}}\int_{−\mathrm{4}} ^{\mathrm{8}} {u}^{\mathrm{2}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \:{cos}^{{n}} \left({u}\right){du}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \:\int_{−\mathrm{4}} ^{\mathrm{8}} \:{u}^{\mathrm{2}} \:{cos}^{{n}} {udu}\:\:\:….{be}\:{continued}… \\ $$
