Menu Close

If-g-x-x-x-and-lim-x-2-f-x-f-2-x-2-ax-b-4-3-find-the-value-of-f-g-1-

Tinku Tara 0 Comments
Pin




Question Number 106309 by bemath last updated on 04/Aug/20
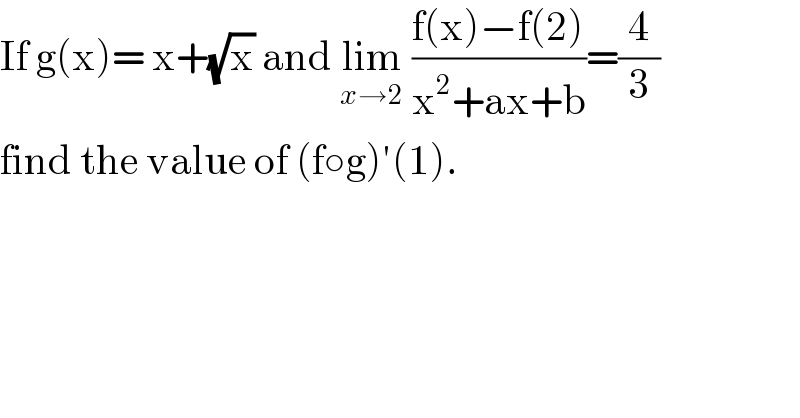
If g(x)= x+(√x) and lim_(x→2) ((f(x)−f(2))/(x^2 +ax+b))=(4/3) find the value of (f○g)′(1).
$$\mathrm{If}\:\mathrm{g}\left(\mathrm{x}\right)=\:\mathrm{x}+\sqrt{\mathrm{x}}\:\mathrm{and}\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{f}\left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{2}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\left(\mathrm{f}\circ\mathrm{g}\right)'\left(\mathrm{1}\right). \\ $$
Answered by bobhans last updated on 05/Aug/20
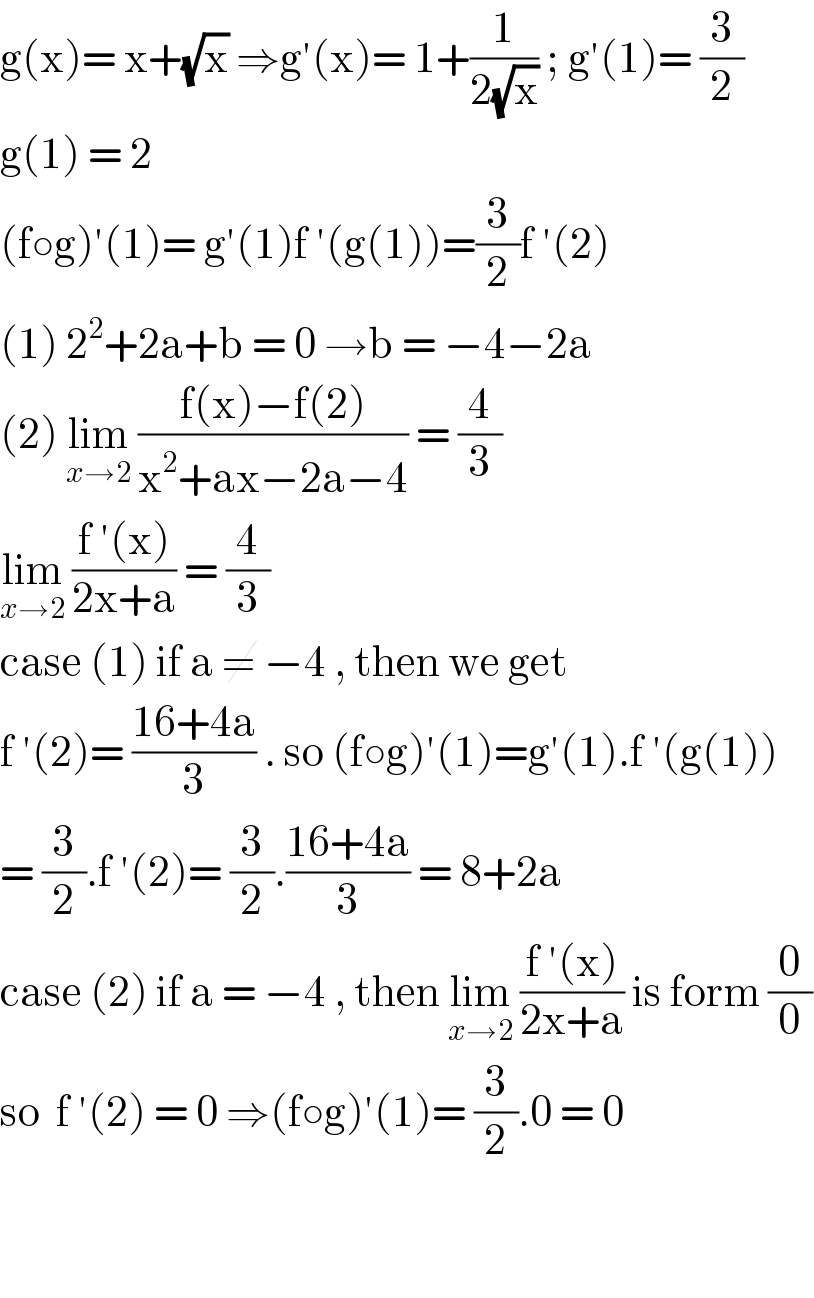
g(x)= x+(√x) ⇒g′(x)= 1+(1/(2(√x))) ; g′(1)= (3/2) g(1) = 2 (f○g)′(1)= g′(1)f ′(g(1))=(3/2)f ′(2) (1) 2^2 +2a+b = 0 →b = −4−2a (2) lim_(x→2) ((f(x)−f(2))/(x^2 +ax−2a−4)) = (4/3) lim_(x→2) ((f ′(x))/(2x+a)) = (4/3) case (1) if a ≠ −4 , then we get f ′(2)= ((16+4a)/3) . so (f○g)′(1)=g′(1).f ′(g(1)) = (3/2).f ′(2)= (3/2).((16+4a)/3) = 8+2a case (2) if a = −4 , then lim_(x→2) ((f ′(x))/(2x+a)) is form (0/0) so f ′(2) = 0 ⇒(f○g)′(1)= (3/2).0 = 0
$$\mathrm{g}\left(\mathrm{x}\right)=\:\mathrm{x}+\sqrt{\mathrm{x}}\:\Rightarrow\mathrm{g}'\left(\mathrm{x}\right)=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\:;\:\mathrm{g}'\left(\mathrm{1}\right)=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{g}\left(\mathrm{1}\right)\:=\:\mathrm{2}\: \\ $$$$\left(\mathrm{f}\circ\mathrm{g}\right)'\left(\mathrm{1}\right)=\:\mathrm{g}'\left(\mathrm{1}\right)\mathrm{f}\:'\left(\mathrm{g}\left(\mathrm{1}\right)\right)=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{f}\:'\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}^{\mathrm{2}} +\mathrm{2a}+\mathrm{b}\:=\:\mathrm{0}\:\rightarrow\mathrm{b}\:=\:−\mathrm{4}−\mathrm{2a} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{f}\left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{2}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{ax}−\mathrm{2a}−\mathrm{4}}\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{f}\:'\left(\mathrm{x}\right)}{\mathrm{2x}+\mathrm{a}}\:=\:\frac{\mathrm{4}}{\mathrm{3}}\: \\ $$$$\mathrm{case}\:\left(\mathrm{1}\right)\:\mathrm{if}\:\mathrm{a}\:\neq\:−\mathrm{4}\:,\:\mathrm{then}\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\mathrm{f}\:'\left(\mathrm{2}\right)=\:\frac{\mathrm{16}+\mathrm{4a}}{\mathrm{3}}\:.\:\mathrm{so}\:\left(\mathrm{f}\circ\mathrm{g}\right)'\left(\mathrm{1}\right)=\mathrm{g}'\left(\mathrm{1}\right).\mathrm{f}\:'\left(\mathrm{g}\left(\mathrm{1}\right)\right) \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{2}}.\mathrm{f}\:'\left(\mathrm{2}\right)=\:\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{16}+\mathrm{4a}}{\mathrm{3}}\:=\:\mathrm{8}+\mathrm{2a} \\ $$$$\mathrm{case}\:\left(\mathrm{2}\right)\:\mathrm{if}\:\mathrm{a}\:=\:−\mathrm{4}\:,\:\mathrm{then}\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{f}\:'\left(\mathrm{x}\right)}{\mathrm{2x}+\mathrm{a}}\:\mathrm{is}\:\mathrm{form}\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\mathrm{so}\:\:\mathrm{f}\:'\left(\mathrm{2}\right)\:=\:\mathrm{0}\:\Rightarrow\left(\mathrm{f}\circ\mathrm{g}\right)'\left(\mathrm{1}\right)=\:\frac{\mathrm{3}}{\mathrm{2}}.\mathrm{0}\:=\:\mathrm{0} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *