Menu Close

if-h-x-x-1-x-x-gt-0-then-h-1-x-

Tinku Tara 0 Comments
Pin




Question Number 164826 by mnjuly1970 last updated on 22/Jan/22
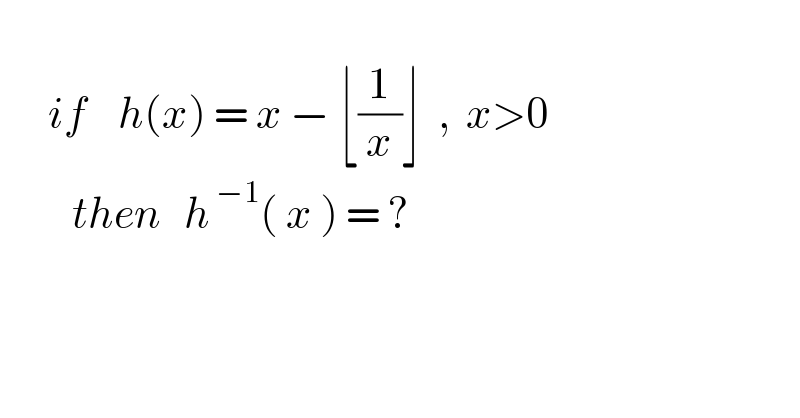
if h(x) = x − ⌊(1/x)⌋ , x>0 then h^( −1) ( x ) = ?
$$ \\ $$$$\:\:\:\:\:\:{if}\:\:\:\:{h}\left({x}\right)\:=\:{x}\:−\:\lfloor\frac{\mathrm{1}}{{x}}\rfloor\:\:,\:\:{x}>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:{then}\:\:\:{h}^{\:−\mathrm{1}} \left(\:{x}\:\right)\:=\:? \\ $$$$ \\ $$
Answered by TheSupreme last updated on 22/Jan/22
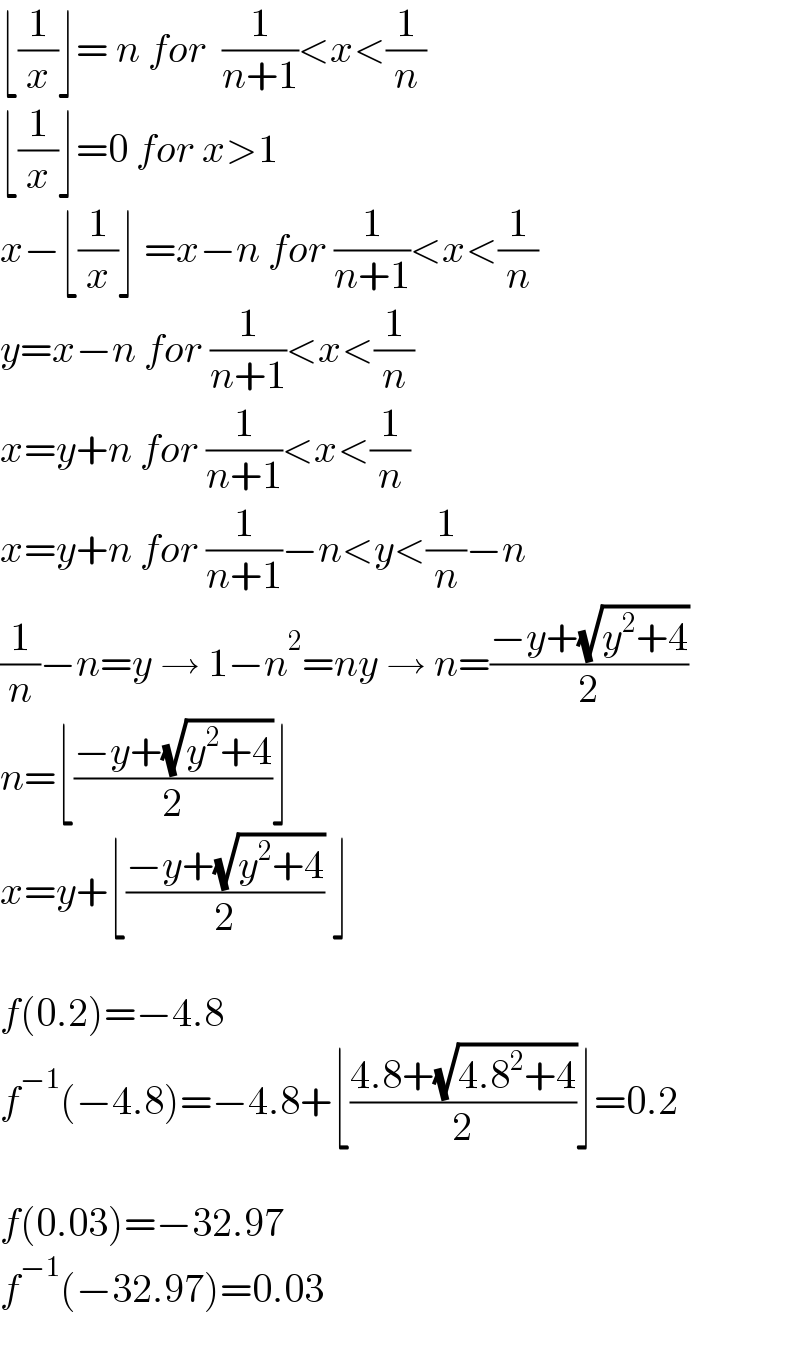
⌊(1/x)⌋= n for (1/(n+1))<x<(1/n) ⌊(1/x)⌋=0 for x>1 x−⌊(1/x)⌋ =x−n for (1/(n+1))<x<(1/n) y=x−n for (1/(n+1))<x<(1/n) x=y+n for (1/(n+1))<x<(1/n) x=y+n for (1/(n+1))−n<y<(1/n)−n (1/n)−n=y → 1−n^2 =ny → n=((−y+(√(y^2 +4)))/2) n=⌊((−y+(√(y^2 +4)))/2)⌋ x=y+⌊((−y+(√(y^2 +4)))/2) ⌋ f(0.2)=−4.8 f^(−1) (−4.8)=−4.8+⌊((4.8+(√(4.8^2 +4)))/2)⌋=0.2 f(0.03)=−32.97 f^(−1) (−32.97)=0.03
$$\lfloor\frac{\mathrm{1}}{{x}}\rfloor=\:{n}\:{for}\:\:\frac{\mathrm{1}}{{n}+\mathrm{1}}<{x}<\frac{\mathrm{1}}{{n}}\: \\ $$$$\lfloor\frac{\mathrm{1}}{{x}}\rfloor=\mathrm{0}\:{for}\:{x}>\mathrm{1} \\ $$$${x}−\lfloor\frac{\mathrm{1}}{{x}}\rfloor\:={x}−{n}\:{for}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}<{x}<\frac{\mathrm{1}}{{n}} \\ $$$${y}={x}−{n}\:{for}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}<{x}<\frac{\mathrm{1}}{{n}} \\ $$$${x}={y}+{n}\:{for}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}<{x}<\frac{\mathrm{1}}{{n}} \\ $$$${x}={y}+{n}\:{for}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}−{n}<{y}<\frac{\mathrm{1}}{{n}}−{n} \\ $$$$\frac{\mathrm{1}}{{n}}−{n}={y}\:\rightarrow\:\mathrm{1}−{n}^{\mathrm{2}} ={ny}\:\rightarrow\:{n}=\frac{−{y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$$${n}=\lfloor\frac{−{y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\rfloor \\ $$$${x}={y}+\lfloor\frac{−{y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\:\rfloor \\ $$$$ \\ $$$${f}\left(\mathrm{0}.\mathrm{2}\right)=−\mathrm{4}.\mathrm{8} \\ $$$${f}^{−\mathrm{1}} \left(−\mathrm{4}.\mathrm{8}\right)=−\mathrm{4}.\mathrm{8}+\lfloor\frac{\mathrm{4}.\mathrm{8}+\sqrt{\mathrm{4}.\mathrm{8}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\rfloor=\mathrm{0}.\mathrm{2} \\ $$$$ \\ $$$${f}\left(\mathrm{0}.\mathrm{03}\right)=−\mathrm{32}.\mathrm{97} \\ $$$${f}^{−\mathrm{1}} \left(−\mathrm{32}.\mathrm{97}\right)=\mathrm{0}.\mathrm{03} \\ $$$$ \\ $$
Answered by mahdipoor last updated on 23/Jan/22
1) x>1 ⇒ y>1 ⇒0<(1/x)<1 ⇒y=x−[(1/x)]=x ⇒h^(−1) (x)=x 2) x=1 ⇒ y=0 ⇒h^(−1) (0)=1 3) 0<x<1 ⇒ y<0 y=x−[(1/x)] ⇒ {y}={x−[(1/x)]} ={x}=x ⇒ h^(−1) (x)=x 1,2,3⇒h^(−1) (x)= { ((x x>1)),((1 x=0 )),(({x} x<0)) :}
$$\left.\mathrm{1}\right)\:{x}>\mathrm{1}\:\Rightarrow\:{y}>\mathrm{1} \\ $$$$\Rightarrow\mathrm{0}<\frac{\mathrm{1}}{{x}}<\mathrm{1}\:\Rightarrow{y}={x}−\left[\frac{\mathrm{1}}{{x}}\right]={x}\:\Rightarrow{h}^{−\mathrm{1}} \left({x}\right)={x} \\ $$$$\left.\mathrm{2}\right)\:{x}=\mathrm{1}\:\Rightarrow\:{y}=\mathrm{0}\:\Rightarrow{h}^{−\mathrm{1}} \left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{0}<{x}<\mathrm{1}\:\Rightarrow\:{y}<\mathrm{0}\: \\ $$$$\:{y}={x}−\left[\frac{\mathrm{1}}{{x}}\right]\:\Rightarrow\:\left\{{y}\right\}=\left\{{x}−\left[\frac{\mathrm{1}}{{x}}\right]\right\}\:=\left\{{x}\right\}={x}\:\Rightarrow \\ $$$$\:{h}^{−\mathrm{1}} \left({x}\right)={x} \\ $$$$\mathrm{1},\mathrm{2},\mathrm{3}\Rightarrow{h}^{−\mathrm{1}} \left({x}\right)=\begin{cases}{{x}\:\:\:\:\:\:\:\:{x}>\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:{x}=\mathrm{0}\:\:}\\{\left\{{x}\right\}\:\:\:{x}<\mathrm{0}}\end{cases} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *