Question Number 152112 by peter frank last updated on 25/Aug/21
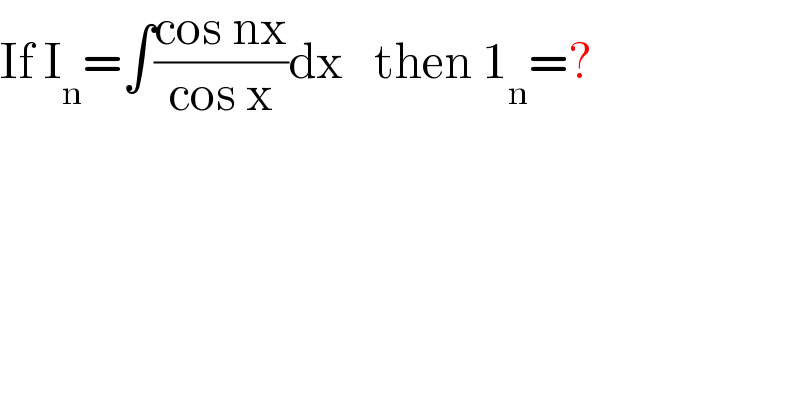
$$\mathrm{If}\:\mathrm{I}_{\mathrm{n}} =\int\frac{\mathrm{cos}\:\mathrm{nx}}{\mathrm{cos}\:\mathrm{x}}\mathrm{dx}\:\:\:\mathrm{then}\:\mathrm{1}_{\mathrm{n}} =? \\ $$
Answered by Olaf_Thorendsen last updated on 26/Aug/21

$$\mathrm{I}_{{n}} \:=\:\int\frac{\mathrm{cos}\left({nx}\right)}{\mathrm{cos}{x}}\:{dx} \\ $$$$\mathrm{I}_{{n}} \:=\:\int\frac{{T}_{{n}} \left(\mathrm{cos}{x}\right)}{\mathrm{cos}{x}}\:{dx} \\ $$$${T}_{{n}} \::\:\mathrm{Tchebychev}\:\mathrm{polynomial} \\ $$$${T}_{{n}} \left({X}\right)\:=\underset{\mathrm{0}\leqslant\mathrm{2}{k}\leqslant{n}} {\sum}\mathrm{C}_{\mathrm{2}{k}} ^{{n}} \left(−\mathrm{1}\right)^{{k}} {X}^{{n}−\mathrm{2}{k}} \left(\mathrm{1}−{X}^{\mathrm{2}} \right)^{{k}} \\ $$$$\mathrm{We}\:\mathrm{must}\:\mathrm{distinguish}\:\mathrm{two}\:\mathrm{cases} \\ $$$${n}\:\mathrm{even}\:\mathrm{and}\:{n}\:\mathrm{odd}… \\ $$
