Question Number 172214 by Shrinava last updated on 24/Jun/22
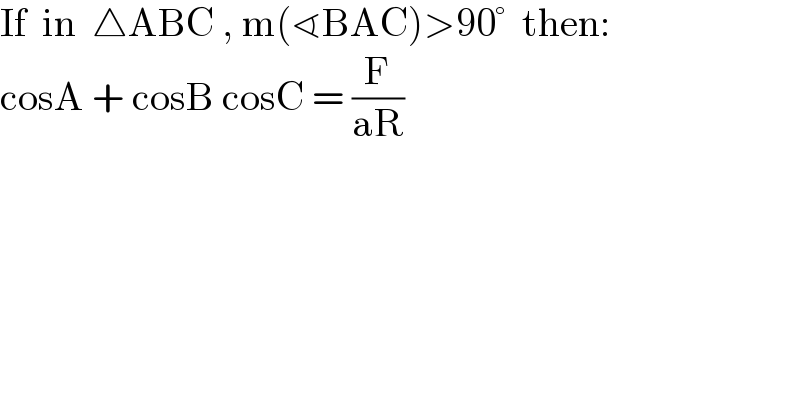
$$\mathrm{If}\:\:\mathrm{in}\:\:\bigtriangleup\mathrm{ABC}\:,\:\mathrm{m}\left(\sphericalangle\mathrm{BAC}\right)>\mathrm{90}°\:\:\mathrm{then}: \\ $$$$\mathrm{cosA}\:+\:\mathrm{cosB}\:\mathrm{cosC}\:=\:\frac{\mathrm{F}}{\mathrm{aR}} \\ $$
Commented by mr W last updated on 24/Jun/22
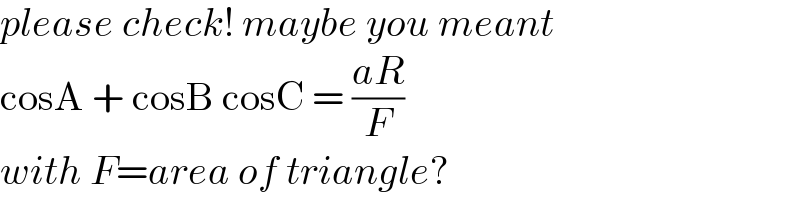
$${please}\:{check}!\:{maybe}\:{you}\:{meant} \\ $$$$\mathrm{cosA}\:+\:\mathrm{cosB}\:\mathrm{cosC}\:=\:\frac{{aR}}{{F}} \\ $$$${with}\:{F}={area}\:{of}\:{triangle}? \\ $$
Commented by Shrinava last updated on 24/Jun/22
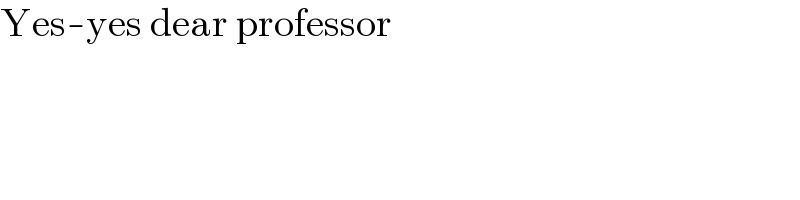
$$\mathrm{Yes}-\mathrm{yes}\:\mathrm{dear}\:\mathrm{professor} \\ $$
Answered by mr W last updated on 24/Jun/22
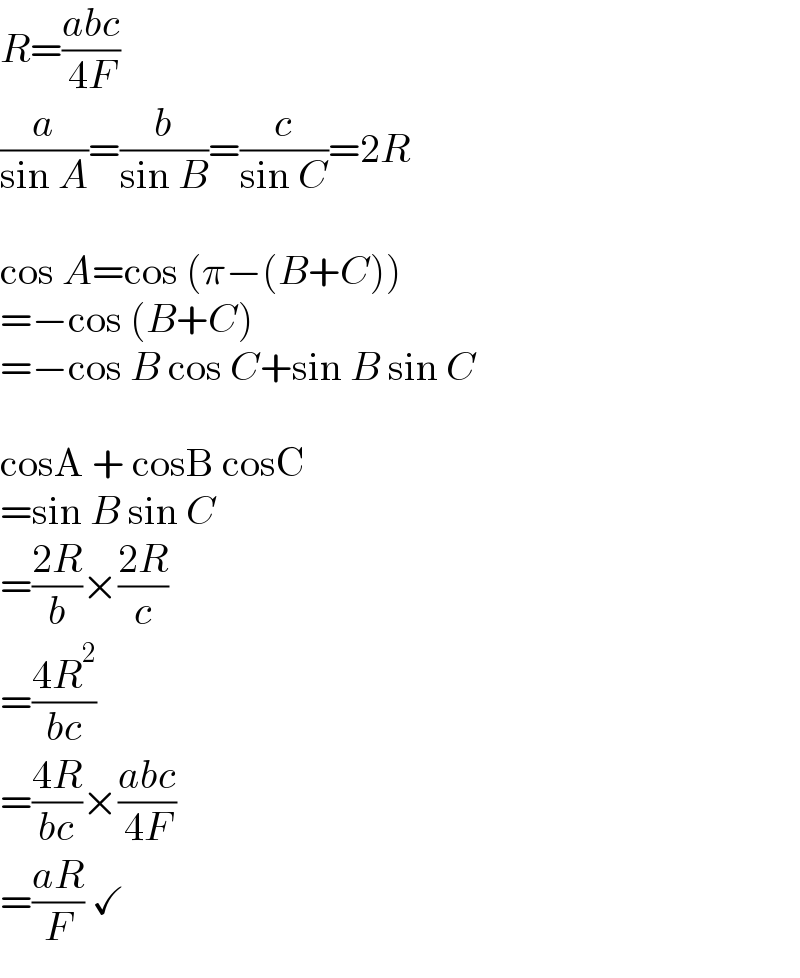
$${R}=\frac{{abc}}{\mathrm{4}{F}} \\ $$$$\frac{{a}}{\mathrm{sin}\:{A}}=\frac{{b}}{\mathrm{sin}\:{B}}=\frac{{c}}{\mathrm{sin}\:{C}}=\mathrm{2}{R} \\ $$$$ \\ $$$$\mathrm{cos}\:{A}=\mathrm{cos}\:\left(\pi−\left({B}+{C}\right)\right) \\ $$$$=−\mathrm{cos}\:\left({B}+{C}\right) \\ $$$$=−\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}+\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$$ \\ $$$$\mathrm{cosA}\:+\:\mathrm{cosB}\:\mathrm{cosC} \\ $$$$=\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$$=\frac{\mathrm{2}{R}}{{b}}×\frac{\mathrm{2}{R}}{{c}} \\ $$$$=\frac{\mathrm{4}{R}^{\mathrm{2}} }{{bc}} \\ $$$$=\frac{\mathrm{4}{R}}{{bc}}×\frac{{abc}}{\mathrm{4}{F}} \\ $$$$=\frac{{aR}}{{F}}\:\checkmark \\ $$
Commented by Sotoberry last updated on 24/Jun/22
$${thankyou}\:{so}\:{much}\:{sir} \\ $$
Commented by Shrinava last updated on 25/Jun/22
$$\mathrm{Cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
