Question Number 16373 by gourav~ last updated on 21/Jun/17
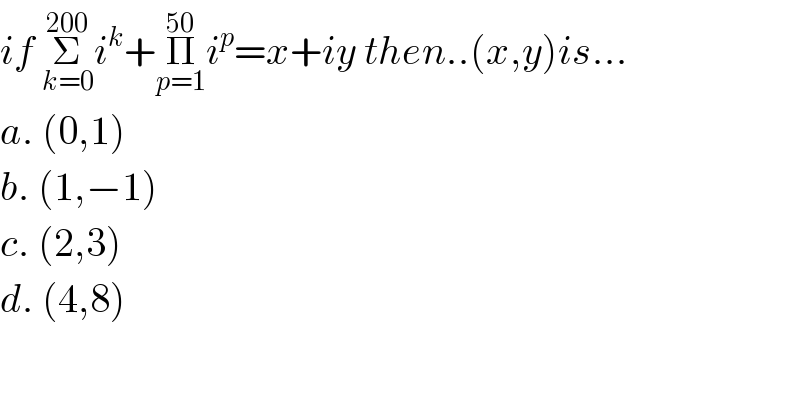
$${if}\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{200}} {\sum}}{i}^{{k}} +\underset{{p}=\mathrm{1}} {\overset{\mathrm{50}} {\prod}}{i}^{{p}} ={x}+{iy}\:{then}..\left({x},{y}\right){is}… \\ $$$${a}.\:\left(\mathrm{0},\mathrm{1}\right) \\ $$$${b}.\:\left(\mathrm{1},−\mathrm{1}\right) \\ $$$${c}.\:\left(\mathrm{2},\mathrm{3}\right) \\ $$$${d}.\:\left(\mathrm{4},\mathrm{8}\right) \\ $$
Commented by gourav~ last updated on 21/Jun/17

$${sir}..\:{plz}\:{solve} \\ $$
Answered by liday last updated on 21/Jun/17
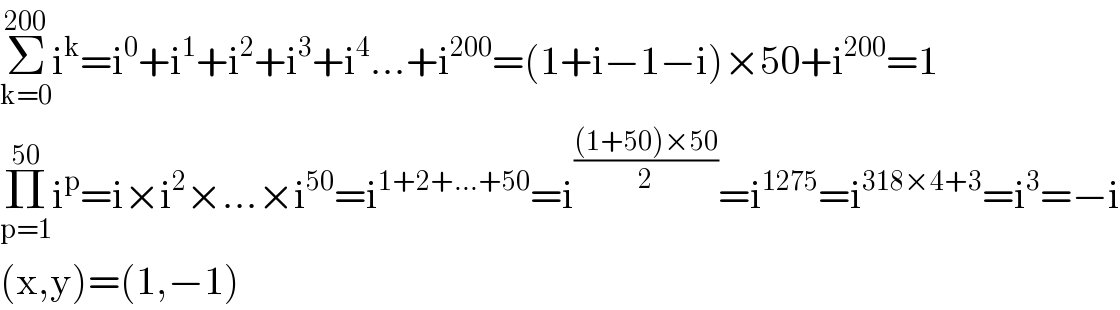
$$\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{200}} {\sum}}\mathrm{i}^{\mathrm{k}} =\mathrm{i}^{\mathrm{0}} +\mathrm{i}^{\mathrm{1}} +\mathrm{i}^{\mathrm{2}} +\mathrm{i}^{\mathrm{3}} +\mathrm{i}^{\mathrm{4}} …+\mathrm{i}^{\mathrm{200}} =\left(\mathrm{1}+\mathrm{i}−\mathrm{1}−\mathrm{i}\right)×\mathrm{50}+\mathrm{i}^{\mathrm{200}} =\mathrm{1} \\ $$$$\underset{\mathrm{p}=\mathrm{1}} {\overset{\mathrm{50}} {\prod}}\mathrm{i}^{\mathrm{p}} =\mathrm{i}×\mathrm{i}^{\mathrm{2}} ×…×\mathrm{i}^{\mathrm{50}} =\mathrm{i}^{\mathrm{1}+\mathrm{2}+…+\mathrm{50}} =\mathrm{i}^{\frac{\left(\mathrm{1}+\mathrm{50}\right)×\mathrm{50}}{\mathrm{2}}} =\mathrm{i}^{\mathrm{1275}} =\mathrm{i}^{\mathrm{318}×\mathrm{4}+\mathrm{3}} =\mathrm{i}^{\mathrm{3}} =−\mathrm{i} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{1},−\mathrm{1}\right) \\ $$
Commented by gourav~ last updated on 21/Jun/17

$${ThNk}\:{u}.. \\ $$
