Menu Close

if-lim-x-0-ae-x-bsin-x-ce-x-xsin-x-2-what-is-a-b-c-

Tinku Tara 0 Comments
Pin




Question Number 80983 by jagoll last updated on 08/Feb/20
if lim_(x→0) ((ae^x −bsin x+ce^(−x) )/(xsin x)) = 2 what is a+b+c ?
$${if}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ae}^{{x}} −{b}\mathrm{sin}\:{x}+{ce}^{−{x}} }{{x}\mathrm{sin}\:{x}}\:=\:\mathrm{2} \\ $$$${what}\:{is}\:{a}+{b}+{c}\:? \\ $$
Commented by jagoll last updated on 09/Feb/20
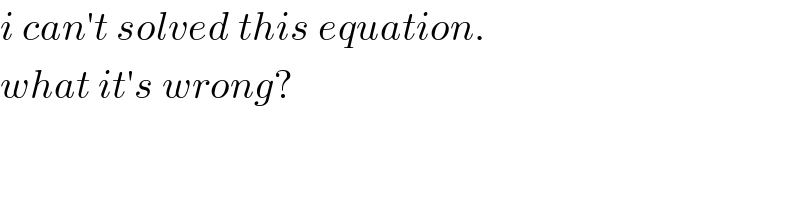
i can′t solved this equation. what it′s wrong?
$${i}\:{can}'{t}\:{solved}\:{this}\:{equation}.\: \\ $$$${what}\:{it}'{s}\:{wrong}? \\ $$
Commented by jagoll last updated on 09/Feb/20
step (1) limit must be (0/0) ⇒a +c = 0 ⇒c = −a step(2) lim_(x→0) ((ae^x −bsin x −ae^(−x) )/(xsin x)) =2 L ^� hopital rule lim_(x→0) ((ae^x −bcos x+ae^(−x) )/(sin x+xcos x)) = 2 since denumerator = 0 , ⇒2a −b = 0 ⇒b = 2a L ^� hopital again lim_(x→0) ((ae^x +bsin x−ae^(−x) )/(2cos x−xsin x))=2 ⇒ (0/2)=2 ⇒?
$${step}\:\left(\mathrm{1}\right)\:{limit}\:{must}\:{be}\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\Rightarrow{a}\:+{c}\:=\:\mathrm{0}\:\Rightarrow{c}\:=\:−{a} \\ $$$${step}\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ae}^{{x}} −{b}\mathrm{sin}\:{x}\:−{ae}^{−{x}} }{{x}\mathrm{sin}\:{x}}\:=\mathrm{2} \\ $$$${L}\hat {\:}{hopital}\:{rule} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ae}^{{x}} −{b}\mathrm{cos}\:{x}+{ae}^{−{x}} }{\mathrm{sin}\:{x}+{x}\mathrm{cos}\:{x}}\:=\:\mathrm{2} \\ $$$${since}\:{denumerator}\:=\:\mathrm{0}\:,\: \\ $$$$\Rightarrow\mathrm{2}{a}\:−{b}\:=\:\mathrm{0}\:\Rightarrow{b}\:=\:\mathrm{2}{a} \\ $$$${L}\hat {\:}{hopital}\:{again} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ae}^{{x}} +{b}\mathrm{sin}\:{x}−{ae}^{−{x}} }{\mathrm{2cos}\:{x}−{x}\mathrm{sin}\:{x}}=\mathrm{2} \\ $$$$\Rightarrow\:\frac{\mathrm{0}}{\mathrm{2}}=\mathrm{2}\:\Rightarrow? \\ $$
Commented by abdomathmax last updated on 09/Feb/20
⇒lim_(x→0) ((ae^x −bsinx +c e^(−x) )/(xsinx))−2=0 ⇒ lim_(x→0) ((a e^x −bsinx+ce^(−x) −2xsinx)/(xsinx))=0⇒ lim_(x→0) u(x)==lim_(x→0) u^′ (x)=0 and lim_(x→0) v(x)=lim_(x→0) v^′ (x)=0 with u(x)=ae^x −bsinx +ce^(−x) −2xsinx ⇒ u(0)=0 ⇒a +c =0 ⇒c=−a u^′ (x)=ae^x −bcosx−ce^(−x) −2sinx−2x cosx u^′ (0)=0 ⇒a−b−c=0 ⇒2a−b=0 ⇒b=2a ⇒a+b+c =2(b+c)=2(2a−a)=2a if we get a=1 ⇒a+b+c=2
$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{ae}^{{x}} −{bsinx}\:+{c}\:{e}^{−{x}} }{{xsinx}}−\mathrm{2}=\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{a}\:{e}^{{x}} −{bsinx}+{ce}^{−{x}} −\mathrm{2}{xsinx}}{{xsinx}}=\mathrm{0}\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {u}\left({x}\right)=={lim}_{{x}\rightarrow\mathrm{0}} {u}^{'} \left({x}\right)=\mathrm{0}\:{and} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {v}\left({x}\right)={lim}_{{x}\rightarrow\mathrm{0}} \:\:{v}^{'} \left({x}\right)=\mathrm{0}\:{with} \\ $$$${u}\left({x}\right)={ae}^{{x}} −{bsinx}\:+{ce}^{−{x}} −\mathrm{2}{xsinx}\:\Rightarrow \\ $$$${u}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow{a}\:+{c}\:=\mathrm{0}\:\Rightarrow{c}=−{a} \\ $$$${u}^{'} \left({x}\right)={ae}^{{x}} −{bcosx}−{ce}^{−{x}} −\mathrm{2}{sinx}−\mathrm{2}{x}\:{cosx} \\ $$$${u}^{'} \left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow{a}−{b}−{c}=\mathrm{0}\:\Rightarrow\mathrm{2}{a}−{b}=\mathrm{0}\:\Rightarrow{b}=\mathrm{2}{a} \\ $$$$\Rightarrow{a}+{b}+{c}\:=\mathrm{2}\left({b}+{c}\right)=\mathrm{2}\left(\mathrm{2}{a}−{a}\right)=\mathrm{2}{a} \\ $$$${if}\:{we}\:{get}\:{a}=\mathrm{1}\:\Rightarrow{a}+{b}+{c}=\mathrm{2} \\ $$
Commented by john santu last updated on 09/Feb/20
you are right sir
$${you}\:{are}\:{right}\:{sir} \\ $$
Commented by jagoll last updated on 09/Feb/20
how to get a = 1 ?
$${how}\:{to}\:{get}\:{a}\:=\:\mathrm{1}\:? \\ $$
Commented by jagoll last updated on 09/Feb/20
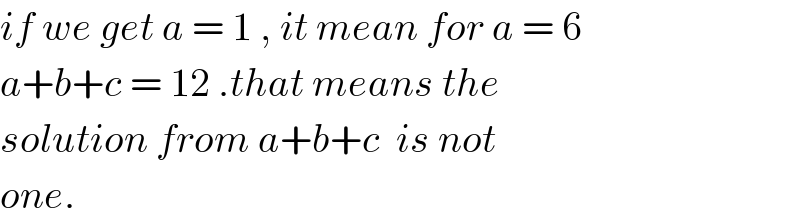
if we get a = 1 , it mean for a = 6 a+b+c = 12 .that means the solution from a+b+c is not one.
$${if}\:{we}\:{get}\:{a}\:=\:\mathrm{1}\:,\:{it}\:{mean}\:{for}\:{a}\:=\:\mathrm{6} \\ $$$${a}+{b}+{c}\:=\:\mathrm{12}\:.{that}\:{means}\:{the} \\ $$$${solution}\:{from}\:{a}+{b}+{c}\:\:{is}\:{not}\: \\ $$$${one}. \\ $$
Commented by mr W last updated on 09/Feb/20
have you checked sir? i don′t think the answer is correct. example: a=1,b=2,c=−1. lim_(x→0) ((e^x −2sin x−e^(−x) )/(xsin x)) =lim_(x→0) ((e^x −2cos x+e^(−x) )/(sin x+x cos x)) =lim_(x→0) ((e^x +2sin x−e^(−x) )/(2 cos x−x sin x)) =(0/2)=0≠2 my answer is: there exist no values for a,b, c such that lim_(x→0) ((ae^x −bsin x+ce^(−x) )/(xsin x))=2.
$${have}\:{you}\:{checked}\:{sir}? \\ $$$${i}\:{don}'{t}\:{think}\:{the}\:{answer}\:{is}\:{correct}. \\ $$$${example}:\:{a}=\mathrm{1},{b}=\mathrm{2},{c}=−\mathrm{1}. \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{2sin}\:{x}−{e}^{−{x}} }{{x}\mathrm{sin}\:{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{2cos}\:{x}+{e}^{−{x}} }{\mathrm{sin}\:{x}+{x}\:\mathrm{cos}\:{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}} +\mathrm{2sin}\:{x}−{e}^{−{x}} }{\mathrm{2}\:\mathrm{cos}\:{x}−{x}\:\mathrm{sin}\:{x}} \\ $$$$=\frac{\mathrm{0}}{\mathrm{2}}=\mathrm{0}\neq\mathrm{2} \\ $$$$ \\ $$$${my}\:{answer}\:{is}: \\ $$$${there}\:{exist}\:{no}\:{values}\:{for}\:{a},{b},\:{c}\:{such} \\ $$$${that}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ae}^{{x}} −{b}\mathrm{sin}\:{x}+{ce}^{−{x}} }{{x}\mathrm{sin}\:{x}}=\mathrm{2}. \\ $$
Commented by jagoll last updated on 09/Feb/20
yes sir. i think it question not right
$${yes}\:{sir}.\:{i}\:{think}\:{it}\:{question}\:{not}\:{right} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *