Question Number 128411 by bramlexs22 last updated on 07/Jan/21
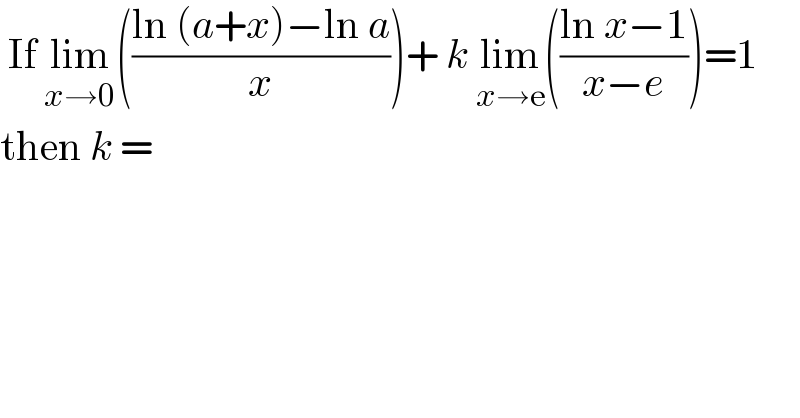
$$\:\mathrm{If}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{ln}\:\left({a}+{x}\right)−\mathrm{ln}\:{a}}{{x}}\right)+\:{k}\:\underset{{x}\rightarrow\mathrm{e}} {\mathrm{lim}}\left(\frac{\mathrm{ln}\:{x}−\mathrm{1}}{{x}−{e}}\right)=\mathrm{1} \\ $$$$\mathrm{then}\:{k}\:=\: \\ $$
Answered by Dwaipayan Shikari last updated on 07/Jan/21
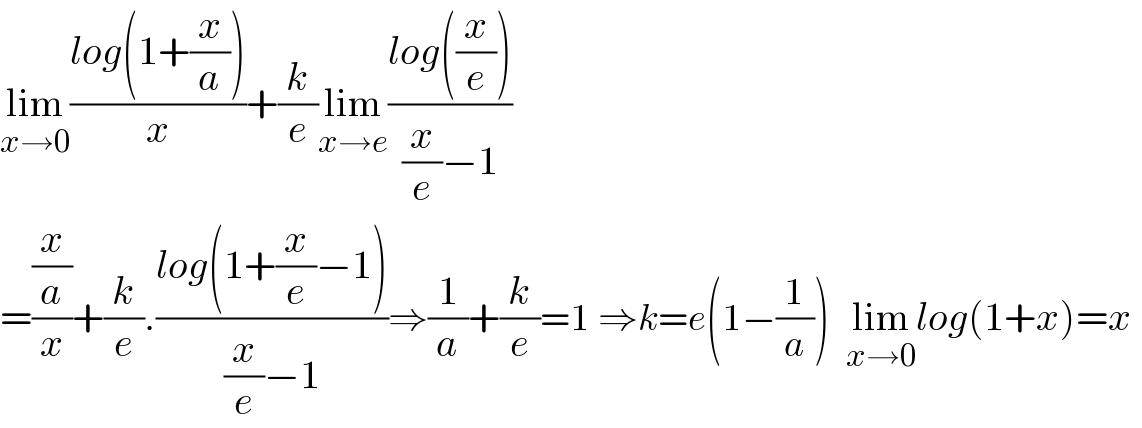
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{log}\left(\mathrm{1}+\frac{{x}}{{a}}\right)}{{x}}+\frac{{k}}{{e}}\underset{{x}\rightarrow{e}} {\mathrm{lim}}\frac{{log}\left(\frac{{x}}{{e}}\right)}{\frac{{x}}{{e}}−\mathrm{1}} \\ $$$$=\frac{\frac{{x}}{{a}}}{{x}}+\frac{{k}}{{e}}.\frac{{log}\left(\mathrm{1}+\frac{{x}}{{e}}−\mathrm{1}\right)}{\frac{{x}}{{e}}−\mathrm{1}}\Rightarrow\frac{\mathrm{1}}{{a}}+\frac{{k}}{{e}}=\mathrm{1}\:\Rightarrow{k}={e}\left(\mathrm{1}−\frac{\mathrm{1}}{{a}}\right)\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{log}\left(\mathrm{1}+{x}\right)={x}\: \\ $$
Answered by mr W last updated on 07/Jan/21

$$\frac{\mathrm{1}}{{a}+\mathrm{0}}+{k}\frac{\mathrm{1}}{{e}}=\mathrm{1} \\ $$$$\Rightarrow{k}=\left(\mathrm{1}−\frac{\mathrm{1}}{{a}}\right){e} \\ $$
Answered by liberty last updated on 07/Jan/21
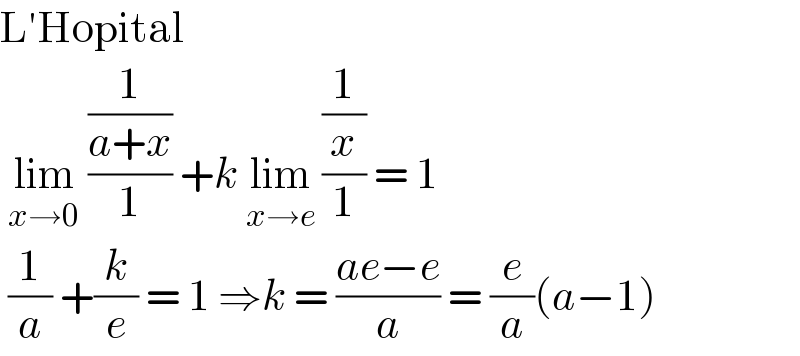
$$\mathrm{L}'\mathrm{Hopital} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{{a}+{x}}}{\mathrm{1}}\:+{k}\:\underset{{x}\rightarrow{e}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{{x}}}{\mathrm{1}}\:=\:\mathrm{1}\: \\ $$$$\:\frac{\mathrm{1}}{{a}}\:+\frac{{k}}{{e}}\:=\:\mathrm{1}\:\Rightarrow{k}\:=\:\frac{{ae}−{e}}{{a}}\:=\:\frac{{e}}{{a}}\left({a}−\mathrm{1}\right) \\ $$
