Question Number 128817 by benjo_mathlover last updated on 10/Jan/21
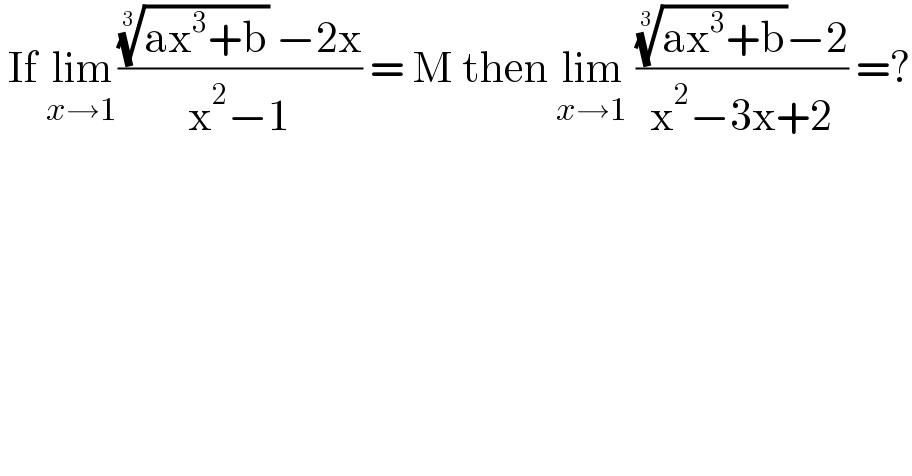
$$\:\mathrm{If}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{ax}^{\mathrm{3}} +\mathrm{b}}\:−\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:=\:\mathrm{M}\:\mathrm{then}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{ax}^{\mathrm{3}} +\mathrm{b}}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}}\:=? \\ $$
Answered by benjo_mathlover last updated on 10/Jan/21
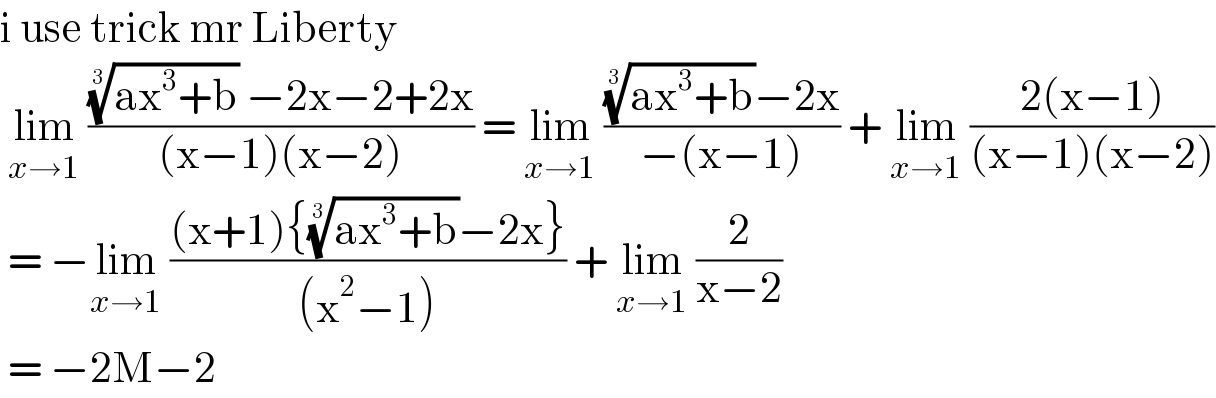
$$\mathrm{i}\:\mathrm{use}\:\mathrm{trick}\:\mathrm{mr}\:\mathrm{Liberty}\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{ax}^{\mathrm{3}} +\mathrm{b}}\:−\mathrm{2x}−\mathrm{2}+\mathrm{2x}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{ax}^{\mathrm{3}} +\mathrm{b}}−\mathrm{2x}}{−\left(\mathrm{x}−\mathrm{1}\right)}\:+\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)} \\ $$$$\:=\:−\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}+\mathrm{1}\right)\left\{\sqrt[{\mathrm{3}}]{\mathrm{ax}^{\mathrm{3}} +\mathrm{b}}−\mathrm{2x}\right\}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}\:+\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{2}}{\mathrm{x}−\mathrm{2}} \\ $$$$\:=\:−\mathrm{2M}−\mathrm{2}\: \\ $$
Commented by liberty last updated on 10/Jan/21

$$\mathrm{hahahaha}….. \\ $$
Answered by rydasss last updated on 11/Jan/21

$${soal}\:{utbk}\:\mathrm{2019} \\ $$
