Menu Close

if-lim-x-1-ax-b-4-x-1-5-find-a-b-

Tinku Tara 0 Comments
Pin




Question Number 181602 by ali009 last updated on 27/Nov/22
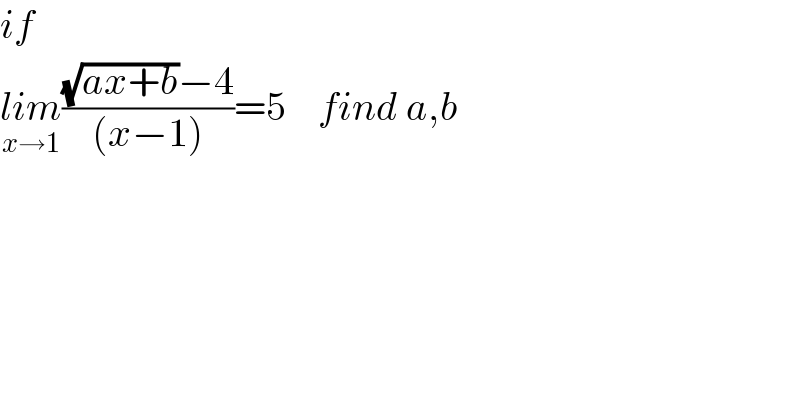
if lim_(x→1) (((√(ax+b))−4)/((x−1)))=5 find a,b
iflimx→1ax+b−4(x−1)=5finda,b
Answered by aleks041103 last updated on 27/Nov/22
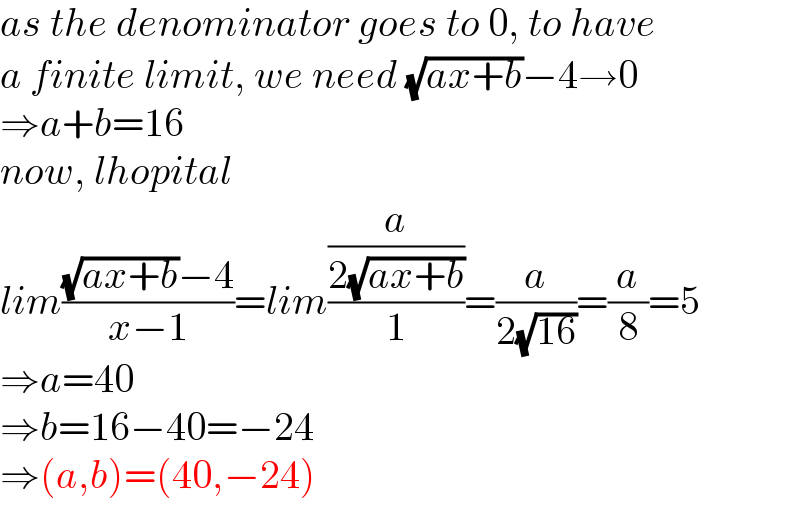
as the denominator goes to 0, to have a finite limit, we need (√(ax+b))−4→0 ⇒a+b=16 now, lhopital lim(((√(ax+b))−4)/(x−1))=lim((a/(2(√(ax+b))))/1)=(a/(2(√(16))))=(a/8)=5 ⇒a=40 ⇒b=16−40=−24 ⇒(a,b)=(40,−24)
asthedenominatorgoesto0,tohaveafinitelimit,weneedax+b−4→0⇒a+b=16now,lhopitallimax+b−4x−1=lima2ax+b1=a216=a8=5⇒a=40⇒b=16−40=−24⇒(a,b)=(40,−24)
Answered by cortano1 last updated on 27/Nov/22
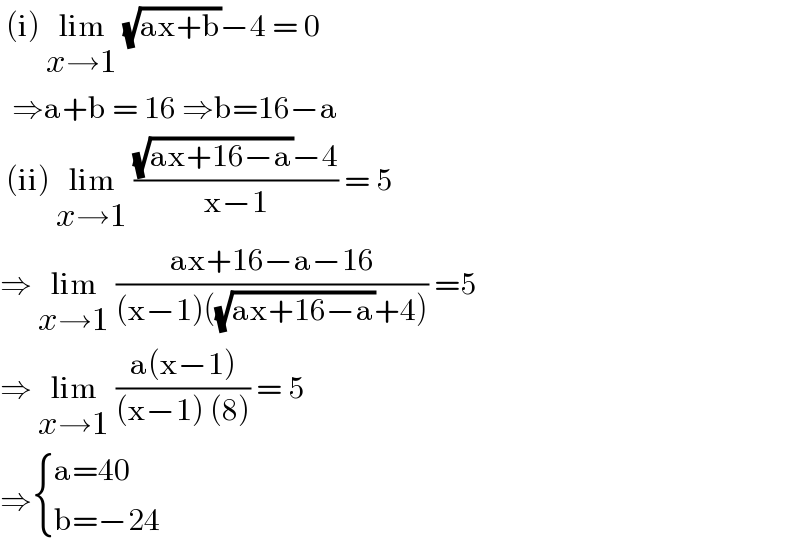
(i) lim_(x→1) (√(ax+b))−4 = 0 ⇒a+b = 16 ⇒b=16−a (ii) lim_(x→1) (((√(ax+16−a))−4)/(x−1)) = 5 ⇒ lim_(x→1) ((ax+16−a−16)/((x−1)((√(ax+16−a))+4))) =5 ⇒ lim_(x→1) ((a(x−1))/((x−1) (8))) = 5 ⇒ { ((a=40)),((b=−24)) :}
(i)limx→1ax+b−4=0⇒a+b=16⇒b=16−a(ii)limx→1ax+16−a−4x−1=5⇒limx→1ax+16−a−16(x−1)(ax+16−a+4)=5⇒limx→1a(x−1)(x−1)(8)=5⇒{a=40b=−24

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *