Menu Close

if-lim-x-1-x-2-ax-b-x-1-5-faind-volve-of-a-b-

Tinku Tara 0 Comments
Pin




Question Number 169204 by mathlove last updated on 26/Apr/22
if lim_(x→1) ((x^2 −ax+b)/(x−1))=5 faind volve of a+b=?
$${if}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} −{ax}+{b}}{{x}−\mathrm{1}}=\mathrm{5} \\ $$$${faind}\:{volve}\:{of}\:{a}+{b}=? \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 26/Apr/22
Do you mean lim_(x→1) ((x^2 −ax+b)/(x−1))=5 ?
$$\mathcal{D}{o}\:{you}\:{mean}\: \\ $$$$\:\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} −{ax}+{b}}{{x}−\mathrm{1}}=\mathrm{5}\:\:\:? \\ $$
Commented by infinityaction last updated on 26/Apr/22
1^(2 ) −a×1 + b = 0 b = 1−a use l hospital rule lim_(x→1) ((2x−a)/1) = 5 2×1 − a =5 a = −3 ∴ b = a−1 b = −3 −1 = −4 then a+b = −4 −3 a+b = −7
$$\:\:\:\:\:\:\mathrm{1}^{\mathrm{2}\:} −{a}×\mathrm{1}\:+\:{b}\:\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:{b}\:\:\:\:=\:\:\mathrm{1}−{a} \\ $$$$\:\:\:{use}\:{l}\:{hospital}\:{rule} \\ $$$$\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}−{a}}{\mathrm{1}}\:=\:\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{2}×\mathrm{1}\:−\:{a}\:=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{a}\:=\:\:−\mathrm{3} \\ $$$$\:\:\:\:\therefore\:\:\:\:\:{b}\:\:=\:{a}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:{b}\:=\:−\mathrm{3}\:−\mathrm{1}\:=\:−\mathrm{4} \\ $$$$\:\:\:{then}\: \\ $$$$\:\:\:\:\:{a}+{b}\:\:=\:\:−\mathrm{4}\:−\mathrm{3} \\ $$$$\:\:\:\:\:{a}+{b}\:\:=\:\:−\mathrm{7} \\ $$$$\: \\ $$
Answered by Rasheed.Sindhi last updated on 26/Apr/22
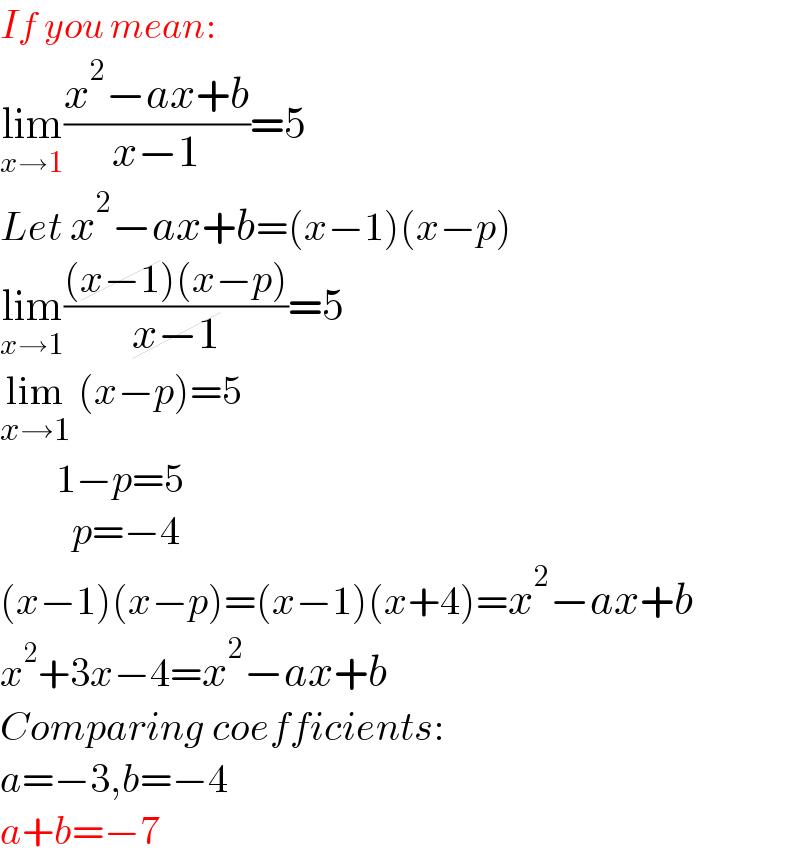
If you mean: lim_(x→1) ((x^2 −ax+b)/(x−1))=5 Let x^2 −ax+b=(x−1)(x−p) lim_(x→1) (((x−1)(x−p))/(x−1))=5 lim_(x→1) (x−p)=5 1−p=5 p=−4 (x−1)(x−p)=(x−1)(x+4)=x^2 −ax+b x^2 +3x−4=x^2 −ax+b Comparing coefficients: a=−3,b=−4 a+b=−7
$${If}\:{you}\:{mean}: \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} −{ax}+{b}}{{x}−\mathrm{1}}=\mathrm{5} \\ $$$${Let}\:{x}^{\mathrm{2}} −{ax}+{b}=\left({x}−\mathrm{1}\right)\left({x}−{p}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left(\cancel{{x}−\mathrm{1}}\right)\left({x}−{p}\right)}{\cancel{{x}−\mathrm{1}}}=\mathrm{5} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left({x}−{p}\right)=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\mathrm{1}−{p}=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:{p}=−\mathrm{4} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}−{p}\right)=\left({x}−\mathrm{1}\right)\left({x}+\mathrm{4}\right)={x}^{\mathrm{2}} −{ax}+{b} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}={x}^{\mathrm{2}} −{ax}+{b}\: \\ $$$${Comparing}\:{coefficients}:\:\:\:\:\:\: \\ $$$${a}=−\mathrm{3},{b}=−\mathrm{4} \\ $$$${a}+{b}=−\mathrm{7} \\ $$
Commented by mathlove last updated on 26/Apr/22
yes x→1
$${yes}\:{x}\rightarrow\mathrm{1} \\ $$
Commented by mathlove last updated on 26/Apr/22
thanks sir alot of
$${thanks}\:{sir}\:{alot}\:{of} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *